- #1
Happiness
- 695
- 31
In the second paragraph after the expression of ##f(u)## below, it wrote "there are three roots to a cubic equation and three combinations of solutions". However, the combination of having three equal real roots was not mentioned. Why?
In the next paragraph, in the second sentence, it wrote "at points ##u=\pm1##, ##f(u)## is always negative, except for the unusual case where ##u=\pm1## is a root". But LHS of (5.62') ##=\dot{u}^2=\dot{\theta}^2\sin^2\theta=0## when ##u=\cos\theta=\pm1##,i.e., ##\theta=0## or ##\pi##. Thus RHS should also be 0. That means ##u=\pm1## is always a root to ##f(u)=0##. What's wrong?

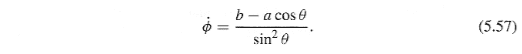



In the next paragraph, in the second sentence, it wrote "at points ##u=\pm1##, ##f(u)## is always negative, except for the unusual case where ##u=\pm1## is a root". But LHS of (5.62') ##=\dot{u}^2=\dot{\theta}^2\sin^2\theta=0## when ##u=\cos\theta=\pm1##,i.e., ##\theta=0## or ##\pi##. Thus RHS should also be 0. That means ##u=\pm1## is always a root to ##f(u)=0##. What's wrong?