Mooorshum
- 5
- 2
- Homework Statement
- I have implemented a finite element geometry of a thin ferromagnetic film with conductive points on it's surface to calculate the current density distribution in the film's volume.
- Relevant Equations
- ∇ ⋅ ( - σ ∇ V) = 0
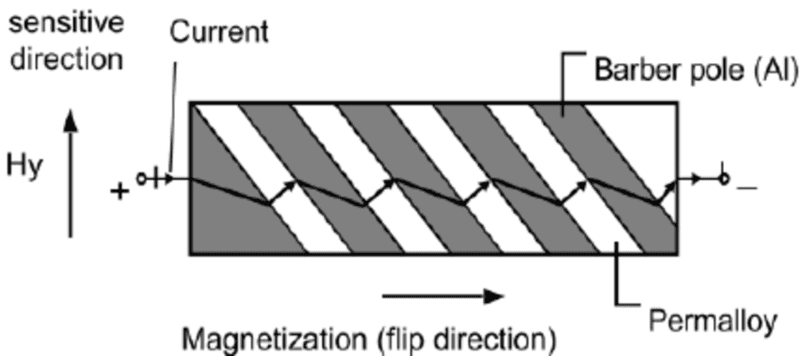
Hi everyone! First time posting here, so I apologize in advance for any bad formatting. I am working on a mathematical model of an anisotropic magnetoresistive sensor. The central part of such a device is a Wheatstone bridge that consists of four current-carrying ferromagnetic (FM) films, the electrical resistance of which changes when an external magnetic field is introduced. An important thing to mention is that typically the current carrying FM film has highly conductive strips added on top of it at a 45 degree angle relative to the long axis of the film. There are multiple reasons for this, but I won't go into any details, as it is not really relevant to the problem at hand. The conductivity of these strips is 1-2 orders higher than that of the FM material, so they act as a shunt, changing the inclination of the current flowing through the film, as can be seen here:
The change in resistivity of the FM film is dependent on the angle
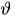 between the current j and magnetization vector M at a certain point of the FM volume, and is governed by the Voigt-Thompson law:
between the current j and magnetization vector M at a certain point of the FM volume, and is governed by the Voigt-Thompson law:
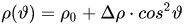 , (1)
, (1)
where
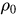 is the resistivity when there is no applied magnetic field,
is the resistivity when there is no applied magnetic field,
 is the change of resistivity (which is proportional to the magnetoresistive ratio of the FM material).
is the change of resistivity (which is proportional to the magnetoresistive ratio of the FM material).
Therefore, to find the resistivity change of a single FM film, we need to know the magnetization and current density distribution in the whole sample.
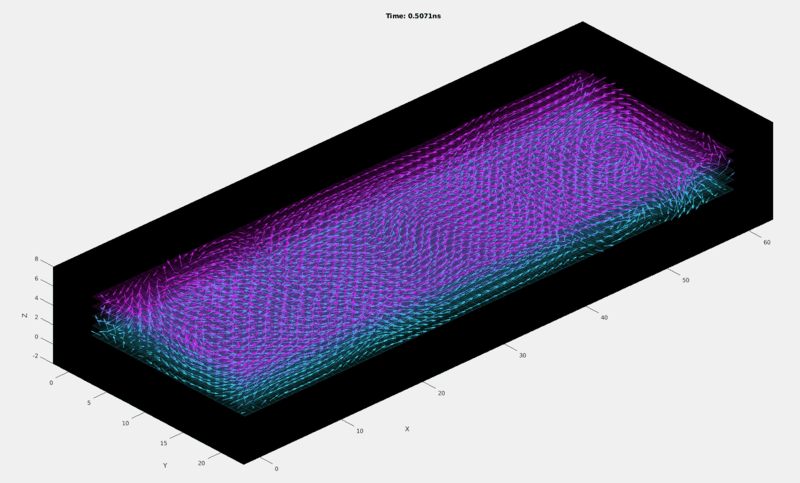
I have implemented a finite element micromagnetic model in matlab, for which I solve the Landau-Lifshitz-Gilbert equation numerically in the constituent cells of the FM film. This allows me to obtain the magnetization configuration for a given external field:
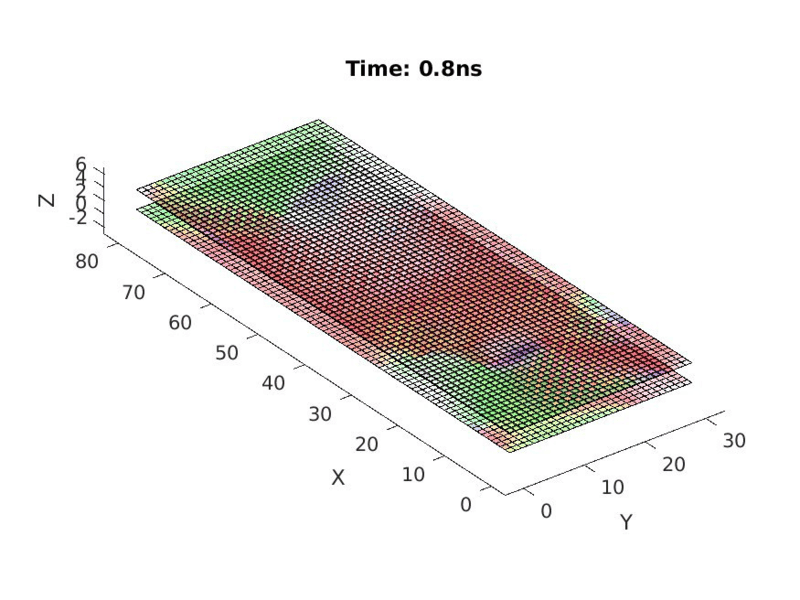
I assume that we have two contact surfaces on opposite parts of the film, between which there is a voltage V0. The voltage is applied to two horizontal strips on top of the film, located at opposite ends of it (these contacts are of the same highly conductive material as the inclined strips). For simplicity, we can assume that one of these strips is grounded:

The electric field can be expressed via the electrostatic potential:
The current density can be expressed as:
We also have the conservation of charge for the electrostatic case:
From Eq. 2, 3, 4 we can derive:
Eq. 5 let's me calculate the electrostatic potential, which lets me find the electric field from Eq. 2, after which I can find the current density distribution via Eq. 3.
Now, Eq. 5 is in the continuous form. To apply it to my finite element geometry, I need to discretize it. If the points in space are denoted by their indices {i, j, k}, then by expanding Eq. 5, and using the finite difference approximations for the first and second order partial derivatives, I can express the electrostatic potential at a given point as:
V{i, j, k} = 1/6 * 1/σ{i, j, k} * ( σ{i+1, j, k} - σ{i-1, j, k} )*( V{i+1, j, k} - V{i-1, j, k} ) / 4h² + σ{i, j, k} * (V{i+1, j, k} + V{i-1, j, k})/h² + ... (6)
(repeated twice, shifting the indices every time) ).
I also have to keep in mind the boundary conditions for V and j:
An important note is that the FM film's conductivity σ is dependent on the local current density. Therefore, I am solving Eq. 6 for a fixed conductivity distribution, then updating the values of j at each point, after which I calculate the new values of σ, and solve Eq. 6 again. This continues until j and σ converge.
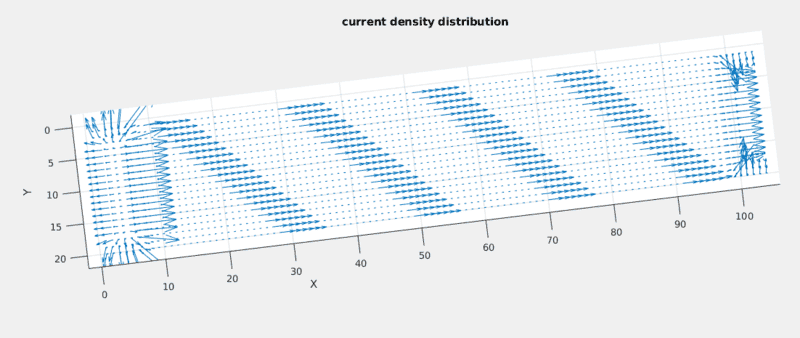
When I implemented this method, I expected to get a current density distribution similar to what is shown in the first picture, however, that is not what I got. Instead of following a zigzag pattern, the current flow seems to be unidirectional, with exceptions near the contact surfaces:
Why could this be happening? I am certain that there is no error in Eq. 6. I have also set the conductivity of the strips at a constant value, so σ only changes in the ferromagnetic portion of the sample. Could I have missed something? Perhaps, the derivation of Eq. 6 is insufficient to describe the shunting effect?
I will be extremely grateful for any tips or suggestions, as I cannot figure out what is wrong.
The change in resistivity of the FM film is dependent on the angle
where
I have implemented a finite element micromagnetic model in matlab, for which I solve the Landau-Lifshitz-Gilbert equation numerically in the constituent cells of the FM film. This allows me to obtain the magnetization configuration for a given external field:
Now I need to calculate the current density distribution in the film, and this is where I am running into some problems.
I assume that we have two contact surfaces on opposite parts of the film, between which there is a voltage V0. The voltage is applied to two horizontal strips on top of the film, located at opposite ends of it (these contacts are of the same highly conductive material as the inclined strips). For simplicity, we can assume that one of these strips is grounded:
The electric field can be expressed via the electrostatic potential:
E = - ∇ V (2)
The current density can be expressed as:
j = σ E, (3)
We also have the conservation of charge for the electrostatic case:
∇ ⋅ j = 0, (4)
From Eq. 2, 3, 4 we can derive:
∇ ⋅ ( - σ ∇ V) = 0 (5).
Eq. 5 let's me calculate the electrostatic potential, which lets me find the electric field from Eq. 2, after which I can find the current density distribution via Eq. 3.
Now, Eq. 5 is in the continuous form. To apply it to my finite element geometry, I need to discretize it. If the points in space are denoted by their indices {i, j, k}, then by expanding Eq. 5, and using the finite difference approximations for the first and second order partial derivatives, I can express the electrostatic potential at a given point as:
V{i, j, k} = 1/6 * 1/σ{i, j, k} * ( σ{i+1, j, k} - σ{i-1, j, k} )*( V{i+1, j, k} - V{i-1, j, k} ) / 4h² + σ{i, j, k} * (V{i+1, j, k} + V{i-1, j, k})/h² + ... (6)
(repeated twice, shifting the indices every time) ).
I also have to keep in mind the boundary conditions for V and j:
- Current cannot flow out any external surface of the sample, except for the contact points, so the normal component of the current density at the boundary faces must be equal to zero.
- The electrostatic potential at the contact surfaces is fixed (V0 and 0 respectively).
An important note is that the FM film's conductivity σ is dependent on the local current density. Therefore, I am solving Eq. 6 for a fixed conductivity distribution, then updating the values of j at each point, after which I calculate the new values of σ, and solve Eq. 6 again. This continues until j and σ converge.
When I implemented this method, I expected to get a current density distribution similar to what is shown in the first picture, however, that is not what I got. Instead of following a zigzag pattern, the current flow seems to be unidirectional, with exceptions near the contact surfaces:
Why could this be happening? I am certain that there is no error in Eq. 6. I have also set the conductivity of the strips at a constant value, so σ only changes in the ferromagnetic portion of the sample. Could I have missed something? Perhaps, the derivation of Eq. 6 is insufficient to describe the shunting effect?
I will be extremely grateful for any tips or suggestions, as I cannot figure out what is wrong.
Last edited: