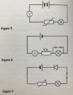
- #1
Jimmy87
- 686
- 17
Homework Statement
[/B]
State and explain whether or not current will flow through the lamps in these circuits
Homework Equations
None
The Attempt at a Solution
I am confused with figure 6 as my explanation is different from my textbook's answer. My textbook says:
"Figure 6 – the lamp is short circuited due to the switch arranged in parallel across it. The current will flow through the switch rather than the lamp due to its far lower resistance".
My explanation would be different. I would say that the LDR will have some significant resistance (which is unknown). The combined resistance of the piece of wire and lamp would be close to zero if you add them reciprocally as they are in parallel and the switch/piece of wire would have a very low resistance. Therefore, the LDR will get all the potential difference and the lamp/wire parallel combo will get none, i.e. no short circuit.
Also, could someone check if my explanation of what would happen if there was no LDR please. If the LDR wasn't there then would the lamp actually work because the lamp is in parallel with the switch and since these would be the only components they would get the full p.d. of the battery? I know in reality the short circuit would cause a huge surge in current and the battery's internal resistance would eat up the p.d. but if we assume there is no internal resistance would the lamp work if the LDR was missing in figure 6?
Thanks.
Attachments
Last edited by a moderator: