Current in relation to magnetic fields and velocity

[Nuru]

Magnetic Field on an incline

This is what looks to be a fairly simple magnetic field problem, but I don't have much experience in relating velocities to electrical currents, so I'm a bit stuck. The problem as described is

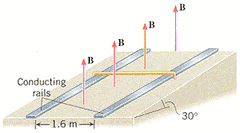
The two conducting rails in the drawing are tilted upwards so they make an angle of 30.0° with respect to the ground. The vertical magnetic field has a magnitude of 0.047 T. The 0.19 kg aluminum rod (length = 1.6 m) slides without friction down the rails at a constant velocity. How much current flows through the bar?

So my variables to my knowledge are
I = unknown
m = 0.19 kg
B = 0.047 T
a = 9.8 m/s (gravity)
L = 1.6 m

The formula I know for this sort of thing is simply $$F = ILB\sin{\theta}$$. My first approach was to use the relation $$F\,=\,MA$$ and substitute that in so I had: $$MA\,=\,ILB\sin{\theta}$$

This turns into $$I\,=\, \frac{MA}{LB\sin{\theta}}$$

So $$I\,=\,\frac{(.19 kg)(9.8 m/s)}{(1.6 m)(0.047 T)\sin{30}}$$

then $$I\,=\,49.5212766$$

However, that obviously isn't right. Did I miss an important detail? I found another problem which was identical except that it had a frictional coefficient they applied in the numerator and they had a $$\theta$$ of 90. Unless I misunderstood something it seems like this should be solvable the same way. Any help would be appreciated.

 

[Nuru]

I think the problem is that I'm using the gravity component in the y-axis instead of for the plane, but I'm not sure how to do that correctly.