Current of delta 3 phase balanced power

[david90]

Hi,

Regarding the picture below, the author calculates L1's current with KCL equation IR-IB = L1. Why is the KCL equation not IR+IB = L1 if the voltage of phase B and Phase R at one point during their cycle can be both positive (Assume positive voltage means current go toward the node)? If Phase B and Phase R voltage are positive then their current move in the same direction and thus IR and IB should have the same signage?

https://www.electricaltechnology.org/2014/09/delta-connection-power-voltage-current.html

 

[Borek]

Isn't it just a matter of convention? Picture clearly shows current directions. You could mark I_B as going up, that would change all equations, giving I_B+I_R for L₁ (that's assuming I understand correctly what L₁ is).

That would also make the system of equations a bit chaotic to my taste though.

 

[david90]

Isn't it just a matter of convention? Picture clearly shows current directions. You could mark I_B as going up, that would change all equations, giving I_B+I_R for L₁ (that's assuming I understand correctly what L₁ is).

That would also make the system of equations a bit chaotic to my taste though.

How can phase shift of L1 be both IB+IR and IB-IR?

 

[DaveE]

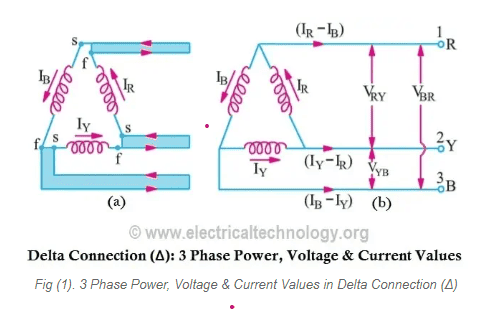
Regarding the picture below, the author calculates L1's current with KCL equation IR-IB = L1. Why is the KCL equation not IR+IB = L1

The author has clearly chosen the current polarities with the indicated arrows. That's why.

It can be an arbitrary choice, you may choose a different definition. But once the choice is made it must be followed.

There is no requirement that the defined current polarities match the voltage polarities. They can be defined separately, arbitrarily.

 

[Babadag]

I agree with DaveE. In order to keep a more clear rule we take R as more than S and S more than T and the direction of current from S to R,from T to S and from R to T.