Current-voltage relation for series association of variable capacitors

[Barloud]

[itex][/itex]Hello,

I have an issue with the problem below.

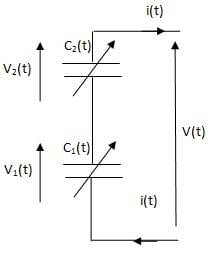
I have a series connection of two variable capacitances $C_{1}(t)$ and $C_{2}(t)$. I want to establish the differential equation between the current i and voltage V on the ports of the series connection.

The capacitance of the series connection of the two capacitors is:

$C_{s}=\frac{C_{1}C_{2}}{C_{1}+C_{2}}$​

The charges on the electrodes of $C_{s}$ are ±$C_{s}V$ and the current i is then

$i=\dot{(C_{s}V)}=\dot{C_{s}}V+C_{s}\dot{V}$​

I use the dot superscript for the time derivative. Using the expression of $C_{s}$ given above, I get the differential equation relating the voltage and current, which is what I am looking for:

$i=\frac{C_{1}^{2} \dot{C_{2}}+C_{2}^{2} \dot{C_{1}}}{(C_{1}+C_{2})^{2}}V+\frac{C_{1}C_{2}}{C_{1}+C_{2}}\dot{V} \; \; \; \; \; \; \; \;Eq.1$​

However, because the problem I describe is just a step in a more complex system that I am studying, I need to understand the method to obtain Eq.1 without knowing in advance that the equivalent series capacitance of $C_{1}$ and $C_{2}$ is equal to $C_{1}C_{2}/(C_{1}+C_{2})$. To do that, I first express the charge on the top electrode of $C_{2}$ as:

$Q=C_{2}V_{2}$​

and the charge on the bottom electrode of $C_{1}$ as:

$-Q=-C_{1}V_{1}$​

For the current, I get:

$i=C_{2}\dot{V_{2}}+V_{2}\dot{C_{2}}=-C_{1}\dot{V_{1}}-V_{1}\dot{C_{1}} \; \; \; \; \; \; \; \;Eq.2$​

And I get stuck here. I am unable to get back to Eq.1 from Eq.2, even by introducing $V=V_{1}+V_{2}$. Any ideas of how I can do that?

 

[UltrafastPED]

even by introducing $V=V_{1}+V_{2}$. Any ideas of how I can do that?

The voltage doesn't change when passing through a capacitor; only the phase changes. Perhaps you should use phasors: http://en.wikipedia.org/wiki/Phasor

So the question is about your voltage/current: is it DC, AC, or something else? If it is DC, then you only have voltage=V.

 

[Barloud]

The voltage and current are AC, as are the variations of the capacitances.
Unfortunately, a method based on complex analysis does not work well here.