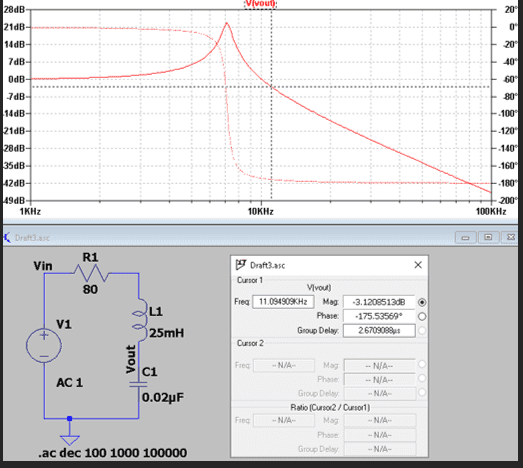
As
@Delta2 pointed out, the link in post #2 is for the case where you are looking at the output voltage across the resistor instead of the capacitor. So, that link does not give the formula for the cutoff frequency for your situation.
As
@DaveE noted in the previous post, finding the -3dB cutoff frequency involves solving the quadratic equation that he wrote down. The solution is a little messy. (I let Mathematica find it!)
$$f_{\rm c.o.} = \frac{1}{2\pi}\left[\frac{1}{LC} - \frac{R^2}{2L^2}+\sqrt{\frac{2}{L^2C^2}-\frac{R^2}{L^3C}+\frac{R^4}{4L^4}} \right]^{1/2}$$ You can plug in your values for ##R, L## and ##C## to see if you get a cutoff frequency of about 11 kHz.