Cylinder pulled by rope on a rough surface

[Karol]

Homework Statement

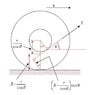
A rope is pulled off with a force F from a combined cylinder. the smaller cylinder's radius is r and the big one's is R. the cylinder rotates on a rough surface without sliding. the force makes an angle θ with the horizon.
What's the acceleration's "a" magnitude and direction.

Homework Equations

Rigid body: $M=I\alpha$
$$I=kMR^2$$

The Attempt at a Solution

Torque relative to the contact point, the torque's arm is:
$$\left( R-\frac{r}{\cos\alpha} \right)\cos\alpha=R\cos\alpha-r$$
$$M=I\alpha\rightarrow F(R\cos\alpha-r)=kMR^2\cdot \alpha,\; R\alpha=a$$
$$\Rightarrow a=R\frac{F(R\cos\alpha-r)}{kMR^2}=\frac{F(R\cos\alpha-r)}{kMR}$$

 

[ehild]

The moment of inertia depends on the position of the rotation axis. You have to specify it. Usually I=kMR² is used with respect to the centre of the rolling body.

 

[Karol]

$$a=R\frac{F(R\cos\alpha-r)}{MR^2(1+k)}=\frac{F(R\cos\alpha-r)}{MR(1+k)}$$