- #1
Leo Liu
- 353
- 156
- Homework Statement
- This is a conceptual question.
- Relevant Equations
- ##\tau = I\alpha##
##F=ma##
##f=\mu F_N##
First we let the static friction coefficient of a solid cylinder (rigid) be ##\mu_s## (large) and the cylinder roll down the incline (rigid) without slipping as shown below, where f is the friction force:
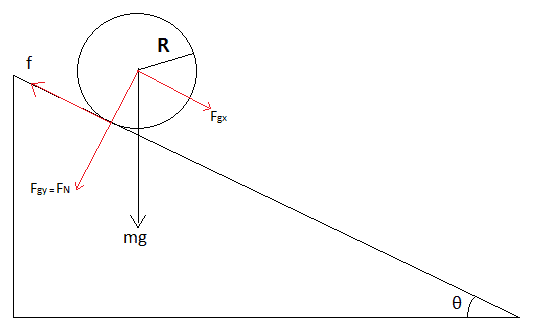
In this case, ##mg\sin(\theta)## is less than ##F_{max}##, where ##F_{CM,max}## is the maximum force (excludes the friction, yet includes the the x component of the gravity ) can be exerted on the cylinder without causing it to slip.
My questions are:
1. How do we calculate the force of friction? Is it equal to ##mg\ cos(\theta) \mu_s## (which is the same as ##f=\frac{1}{2}ma_{CM,max}##) or ##f=\frac{1}{2}ma_{CM}##? (please note that the ##a## in the latter is a variable)
2. What is the norm of translational acceleration ##a## in this example?
3. If the cylinder does slip when rolling down, how would you find the force of friction? Do you need any additional information?
Derivation of the formula in question 1:
$$\tau = I\alpha$$
$$Rf\sin(90) = \frac{1}{2}mR^2 \frac{d\omega}{dt}$$
$$f=\frac{1}{2}m\frac{d\omega R}{dt}=\frac{1}{2}m\frac{dv_{tan}}{dt}=\frac{1}{2}ma_{tan}=\frac{1}{2}ma_{CM}$$
In this case, ##mg\sin(\theta)## is less than ##F_{max}##, where ##F_{CM,max}## is the maximum force (excludes the friction, yet includes the the x component of the gravity ) can be exerted on the cylinder without causing it to slip.
My questions are:
1. How do we calculate the force of friction? Is it equal to ##mg\ cos(\theta) \mu_s## (which is the same as ##f=\frac{1}{2}ma_{CM,max}##) or ##f=\frac{1}{2}ma_{CM}##? (please note that the ##a## in the latter is a variable)
2. What is the norm of translational acceleration ##a## in this example?
3. If the cylinder does slip when rolling down, how would you find the force of friction? Do you need any additional information?
Derivation of the formula in question 1:
$$\tau = I\alpha$$
$$Rf\sin(90) = \frac{1}{2}mR^2 \frac{d\omega}{dt}$$
$$f=\frac{1}{2}m\frac{d\omega R}{dt}=\frac{1}{2}m\frac{dv_{tan}}{dt}=\frac{1}{2}ma_{tan}=\frac{1}{2}ma_{CM}$$
Last edited: