Cylinder rolling inside a moving pipe

[CAF123]

Homework Statement

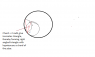
A thin-walled pipe with mass M and radius R (moment of inertia MR²) rolls without slipping on a horizontal surface. Inside the pipe, a solid cylinder of mass m and radius r (moment of inertia (1/2)mr²) also rolls without slipping under gravity. $\alpha$ and $\phi$ are, respectively, the angles through which the pipe and cylinder rotate about their centres, and $θ$ is the angular displacement of the centre of the cylinder from the downward vertical through the centre of the pipe. All three angles should be chosen so that they are zero for a configuration in which the cylinder is at the bottom of the pipe, and all three should increase in the same sense, i.e., either all clockwise, or all anticlockwise.

The questions and an illustration are given in the attachment.

Homework Equations

Lagrange Equations, kinetic and potential energies.

The Attempt at a Solution

I'll repeat the questions here.

a)Find the holonomic constraint relating the angles
I got that the holonomic constraint between the angles was $\alpha - \theta = \phi/2$ after some geometry.

b)Show that, in the C.O.M frame of the cylinder, the cylinder rotates through an angle $\theta + \phi$.
That is obvious, but I am not sure what the question wants me to say. In the frame co-moving with the centre of the cylinder, it sees the centre of mass of the cylinder sketch out an arc of a circle of radius R-r. From the vertical through the pipe, the angle to a point on the cylinder is then $\theta + \phi$. ($\theta$ takes you to the vertical through the cylinder and $\phi$ then takes you to a point on the cylinder, so relative to the zero angle, it is the sum.)

c)Find the kinetic energies of the pipe and cylinder.
I managed to obtain the correct expression for the pipe, but the cylinder I did not.
The general expression for $T = T' + V \cdot P' + \frac{1}{2}MV^2$, where T the kinetic energy in frame S, T' in frame S' and V the relative speed of the frames.

Let S' be the frame co-moving with the centre of the pipe. Then, $T' = \frac{1}{2}m((R-r)(\dot{\theta}+\dot{\phi}))^2 + \frac{1}{2} (\frac{1}{2}mr^2) (\dot{\theta}+\dot{\phi})^2$. Since there is no slip of the pipe, $\mathbf{V} = R\dot{\alpha}\underline{e}_x$ and $P' = P - (M+m)V$, where $P = MR\dot{\alpha} + m2r(\dot{\theta}+\dot{\phi})$ is the momentum of the C.O.M of the pipe and cylinder respectively, relative to S.

Many thanks.

 

[mfb]

a)Find the holonomic constraint relating the angles
I got that the holonomic constraint between the angles was α−θ=ϕ/2 after some geometry.

That equation should depend on R and r somehow. This is easier to see with θ=0, the cylinder on the bottom of the pipe.

I agree with (b).

I don't understand the second part of your work in (c) (after "Since there is no slip").

 

[CAF123]

Hi mfb,

That equation should depend on R and r somehow. This is easier to see with θ=0, the cylinder on the bottom of the pipe.

That makes sense, all angles should vanish when the cylinder is at the bottom. I can figure things in terms of arc lengths so that $R\alpha = R \theta + R \phi/2$ but that doesn't involve $r$ nor give me the correct limiting value.

I don't understand the second part of your work in (c) (after "Since there is no slip").

I was trying to calculate T in S from the transformation law $T = T' + (1/2)MV^2 + V \cdot P'$. I identified a possible S' to be the frame co-moving with the centre of the pipe. Then the velocity of the centre of the pipe V, is $V=R\dot{\alpha}$, from which I can get one of the terms (1/2)MV², where M in this problem is the combined mass M + m, I think.

T' is the kinetic energy in S'. This will consist of translational kinetic energy of the C.O.M of the cylinder + motion about the C.O.M of the cylinder (i.e rotation) which gives me $\frac{1}{2}m((R-r)(\dot{\theta}+\dot{\phi})^2 + \frac{1}{2} (\frac{1}{2}mr^2) (\dot{\theta}+\dot{\phi})^2$

Now I need $V \cdot P'$. I used the momentum transformation law: P' = P - MV, where again M means M+m in this problem. In S, there is momentum contribution from the translational motion of both the pipe and the cylinder. So for the pipe, I have that $P_{pipe} = MR\dot{\alpha}$ and for the cylinder $P_{cyl} = mr(\dot{\theta}+\dot{\phi})$. (I obtained these momentum values by considering the C.O.M's as point particles, with all mass there).

 

[mfb]

That makes sense, all angles should vanish when the cylinder is at the bottom. I can figure things in terms of arc lengths so that $R\alpha = R \theta + R \phi/2$ but that doesn't involve $r$ nor give me the correct limiting value.

One of those R has to be an r as it is the length along the small cylinder.

I was trying to calculate T in S from the transformation law $T = T' + (1/2)MV^2 + V \cdot P'$. I identified a possible S' to be the frame co-moving with the centre of the pipe. Then the velocity of the centre of the pipe V, is $V=R\dot{\alpha}$, from which I can get one of the terms (1/2)MV², where M in this problem is the combined mass M + m, I think.

Focus on the inner cylinder first, please. Adding the pipe makes things more complicated, it is way easier to calculate it separately.
I did not understand the notation $\mathbf{V} = R\dot{\alpha}\underline{e}_x$, and this part is one-dimensional anyway.

T' is the kinetic energy in S'. This will consist of translational kinetic energy of the C.O.M of the cylinder + motion about the C.O.M of the cylinder (i.e rotation) which gives me $\frac{1}{2}m((R-r)(\dot{\theta}+\dot{\phi})^2 + \frac{1}{2} (\frac{1}{2}mr^2) (\dot{\theta}+\dot{\phi})^2$

Where does the $\dot{\phi}$ in the second term come from?

Now I need $V \cdot P'$. I used the momentum transformation law: P' = P - MV, where again M means M+m in this problem. In S, there is momentum contribution from the translational motion of both the pipe and the cylinder. So for the pipe, I have that $P_{pipe} = MR\dot{\alpha}$ and for the cylinder $P_{cyl} = mr(\dot{\theta}+\dot{\phi})$. (I obtained these momentum values by considering the C.O.M's as point particles, with all mass there).[/QUOTE]

I used the momentum transformation law: P' = P - MV, where again M means M+m in this problem.

You just have the inner cylinder here.

(I obtained these momentum values by considering the C.O.M's as point particles, with all mass there).

Okay, but to calculate V*P' you have to consider their directions.

 

[CAF123]

One of those R has to be an r as it is the length along the small cylinder.

It makes sense for that to be the case but, by looking at the sketch, the arc of the circle $R\alpha$ is equal to the arc $R\theta$ + arc $R(\alpha-\theta)$ (or $R(\phi/2)$).

Focus on the inner cylinder first, please. Adding the pipe makes things more complicated, it is way easier to calculate it separately.

Ok, so the equation is $T_{cyl} = T'_{cyl} + (V \cdot P')_{cyl} + \frac{1}{2}mV^2$. The first term is the kinetic energy of the cylinder about the centre of the pipe. That is $\frac{1}{2}m((R-r)(\dot{\theta})^2$ + $\frac{1}{2}(\frac{1}{2}mr^2) (\dot{\theta})^2.$ I don't think there is a $\dot{\phi}$ term here since $\theta$ is the angle from the vertical to the centre of mass of the cylinder.

The last term on the RHS is the translational kinetic energy of the cylinder as viewed from frame S, where V is the relative velocity of the cylinder and S. So that would be $\frac{1}{2}m(R\dot{\alpha})^2$ since the cylinder is inside the pipe which has translational speed $R\dot{\alpha}$.

Now I need $V \cdot P'$. Using the momentum transformation law: P' = P - MV, I have that $MV = mR\dot{\alpha}$ and P is the momentum of the cylinder relative to S. This will be $mR\dot{\alpha} + m(R-r)\dot{\theta}^2$.

 

[CAF123]

Let me try to do this without invoking the momentum transformation law and do it by more geometry. I will go back to the other method after I have the correct expression this way.

The velocity vector of the centre of mass of the cylinder relative to the centre of the pipe is given by $\underline{v'} = -((R-r)\dot{\theta} \cos \theta)\underline{e}_x + (R-r)\dot{\theta} \sin \theta \underline{e}_y$ A Galilean transformation gives the velocity to an inertial frame $\underline{v} = -((R-r)\dot{\theta} \cos \theta + R\dot{\alpha})\underline{e}_x + (R-r)\dot{\theta} \sin \theta \underline{e}_y$. Multiply by $m$ to get the momentum and dot this with the translational speed of S', which is $\underline{V} = R\dot{\alpha}\underline{e}_x$. The result is $-R\dot{\alpha}(R-r)\dot{\theta} \cos{\theta} - R^2 \dot{\alpha}^2$

Then the two other terms are kinetic energy in frame S' given by $$\frac{1}{2}m ((R-r)\dot{\theta})^2 + \frac{1}{2}(\frac{1}{2}mr^2)\dot{\theta}^2$$ and a final translational term $\frac{1}{2}m(R \dot{\alpha})^2$. I still think I am missing some terms though. Thanks.

 

[CAF123]

I seem to still be missing a term from the second term of $T_{cylinder}$ in the question. I don't quite get the factors 3m/4 either. Thanks.

 

[TSny]

A Galilean transformation gives the velocity to an inertial frame $\underline{v} = -((R-r)\dot{\theta} \cos \theta + R\dot{\alpha})\underline{e}_x + (R-r)\dot{\theta} \sin \theta \underline{e}_y$.

I don't quite agree with all the signs here. Note that the problem asks you to choose all angles positive in the CCW direction, or all angles positive in the CW direction. Suppose you choose all angles positive in the CCW direction. [$\theta$ then has a negative value in the original diagram of the problem.] Then a positive $\dot{\theta}$ will give the center of the cylinder a positive x-component of velocity as well as a positive y-component of velocity if $\theta$ is postive. A positive $\dot{\alpha}$ will contribute a negative x-component of velocity of the center of the cylinder. This agrees with all of your signs except for the $-(R-r)\dot{\theta} \cos \theta$ part of your x-component of velocity which you have as negative. I hope I'm not overlooking a sign.

The total KE of the cylinder is the KE due to the translational motion of the CM plus the KE due to rotation about the CM.

The translational KE is just $\frac{1}{2}m(v_x^2 + v_y^2)$ using the x and y components of your velocity $\underline{v}$

The rotational KE about the CM of the cylinder is $\frac{1}{2}I(\dot{\theta}^2+\dot{\phi}^2)$.

You still need to get the correct holonomic constraint relating $\phi, \theta$ and $\alpha$.
Then you can substitute for $\dot{\phi}$ in terms of $\dot{\theta}$ and $\dot{\alpha}$.

 

[CAF123]

Hi TSny, thanks for reply.

I don't quite agree with all the signs here. Note that the problem asks you to choose all angles positive in the CCW direction, or all angles positive in the CW direction. Suppose you choose all angles positive in the CCW direction. [$\theta$ then has a negative value in the original diagram of the problem.] Then a positive $\dot{\theta}$ will give the center of the cylinder a positive x-component of velocity as well as a positive y-component of velocity if $\theta$ is postive. A positive $\dot{\alpha}$ will contribute a negative x-component of velocity of the center of the cylinder. This agrees with all of your signs except for the $-(R-r)\dot{\theta} \cos \theta$ part of your x-component of velocity which you have as negative. I hope I'm not overlooking a sign.

I chose my angles to measured positively in the CW direction, but indeed I messed up one of the signs. $\underline{v} = (-(R-r)\dot{\theta}\cos \theta + R\dot{\alpha})\underline{e}_x + (R-r)\dot{\theta} \sin \theta\underline{e}_y$

The total KE of the cylinder is the KE due to the translational motion of the CM plus the KE due to rotation about the CM.
The translational KE is just $\frac{1}{2}m(v_x^2 + v_y^2)$ using the x and y components of your velocity $\underline{v}$

That is because in the general expression T = T' + V.P' + (1/2)mv², you have taken S' to be the C.O.M of the pipe and so P'=0. T' is then the rotational kinetic energy about S' and (1/2)mv² is the translational kinetic energy you mentioned. The sum of which gives T. And in this case, V.P' is not 0 (where P' is the momentum of the cylinder wrt S') since all velocity vectors on the rim of the cylinder cancel in S'. The only velocity vector that does not cancel is the velocity vector of the centre. So, $$V \cdot P' = (R\dot{\alpha})\underline{e}_x \cdot m(-(R-r)\dot{\theta}\cos \theta \underline{e}_x + R\dot{\theta}\sin \theta \underline{e}_y = -m(R-r)R \cos \theta \dot{\alpha} \dot{\theta}$$ although I seem to be overcounting terms (since the translational kinetic energy term gives me this term too)

The rotational KE about the CM of the cylinder is $\frac{1}{2}I(\dot{\theta}^2+\dot{\phi}^2)$.

I don't quite follow this expression. If the angle to a point on the surface is $\theta+\phi$ then the angular velocity is the time derivative: $\omega = \dot{\theta} + \dot{\phi}$. In the generic expression, (1/2)Iω², this means $\omega^2 = (\dot{\theta} + \dot{\phi})^2$, no?

You still need to get the correct holonomic constraint relating $\phi, \theta$ and $\alpha$.

$R{\alpha}$ gives the longest arc length. But this is equal to the sum of the arc lengths $R{\theta}$ and $R(\alpha - \theta) = R(\phi/2)$. $r\phi$ would be the arc length of the cylinder, but I don't think that helps.

Thanks.

 

[TSny]

I don't quite follow this expression. If the angle to a point on the surface is $\theta+\phi$ then the angular velocity is the time derivative: $\omega = \dot{\theta} + \dot{\phi}$. In the generic expression, (1/2)Iω², this means $\omega^2 = (\dot{\theta} + \dot{\phi})^2$, no?

You are absolutely correct. I wasn't thinking when I typed this expression, but I had it correct in my calculations. I get the expression for $T_{cyl}$ given in the statement of the problem if I just add the translational KE of the CM $$T_{tran}=\frac{1}{2}m(v_x^2+v_y^2)$$ plus the rotational KE about the cm $$T_{rot} = \frac{1}{2}I( \dot{\theta}+\dot{\phi})^2$$
I haven't followed your use of the momentum P. I tried to work everything out from the point of view of the fixed Earth inertial frame in which both the pipe and the cylinder are moving. The KE of the cylinder relative to the Earth is the KE due to motion of the CM relative to the Earth plus the KE due to rotation about the CM.

What did you get for the holonomic constraint that relates $\theta$, $\phi$, and $\alpha$?

 

[CAF123]

I get the expression for $T_{cyl}$ given in the statement of the problem if I just add the translational KE of the CM $$T_{tran}=\frac{1}{2}m(v_x^2+v_y^2)$$ plus the rotational KE about the cm $$T_{rot} = \frac{1}{2}I( \dot{\theta}+\dot{\phi})^2$$

That makes sense. When you refer to the 'CM' do you mean the centre of mass of the cylinder? In which case, I agree, in that frame P' = 0 (by definition) and the expression for kinetic energy relative to the Earth is the translational kinetic energy of the cylinder and the kinetic energy about the centre of the cylinder.

What did you get for the holonomic constraint that relates $\theta$, $\phi$, and $\alpha$?

Using geometry I get that the angle $\alpha - \theta = \phi/2$. But this does not produce the correct limiting value. When the cylinder is at the bottom of the pipe, $\theta=0$ and so by my equation I get that $2\alpha = \phi$, but I think I want all the angles to vanish identically.

In dealing with arc lengths, I got that $R\alpha = R\theta + R(\alpha-\theta) = R\theta + R\phi/2$, but again this does not give correct limiting results.

Thanks.

 

[TSny]

That makes sense. When you refer to the 'CM' do you mean the centre of mass of the cylinder?

Yes, that's right.

Using geometry I get that the angle $\alpha - \theta = \phi/2$. But this does not produce the correct limiting value. When the cylinder is at the bottom of the pipe, $\theta=0$ and so by my equation I get that $2\alpha = \phi$, but I think I want all the angles to vanish identically.

In dealing with arc lengths, I got that $R\alpha = R\theta + R(\alpha-\theta) = R\theta + R\phi/2$, but again this does not give correct limiting results.

As mfb noted earlier, your constraint relating $\alpha, \theta$, and $\phi$ should involve both $r$ and $R$. Deriving this relation was the hardest part for me. I first assumed $\alpha$ was fixed at zero and worked out a constraint between $\theta$ and $\phi$. I then had to think about how this would be modified if $\alpha \neq 0$.

 

[CAF123]

As mfb noted earlier, your constraint relating $\alpha, \theta$, and $\phi$ should involve both $r$ and $R$. Deriving this relation was the hardest part for me. I first assumed $\alpha$ was fixed at zero and worked out a constraint between $\theta$ and $\phi$. I then had to think about how this would be modified if $\alpha \neq 0$.

I did not get the result, but could you tell me if these are some observations that would help: Two radii of the cylinder and a chord of the cylinder produce an isosceles triangle. This chord and a chord of the pipe, together with a portion of a radius of the pipe give a right angled triangle. I am trying to find angles that would relate to the total circumferential length of the cylinder. $r\phi$ gives a small arc length, but I can't seem to find any angles that would give me the rest. A point on the rim of the cylinder relative to the centre of the cylinder is $\phi$. The same point relative to the centre of the pipe is $\theta + \phi$.

 

[TSny]

I think I would need a picture to see what you are saying.

Here is a figure that I used. A subscript o on an angle indicates that the angle is for the case where $\alpha = 0$. I did not put a subscript on $\phi$ since it is not affected by $\alpha$. $\phi$ is the angle between the blue and green stripes. I chose all angles as positive in the CCW direction.

On the left, the cylinder is imagined to rotate along a horizontal line. This figure is then imagined wrapped along the pipe as shown on the right. Wrapping along the pipe causes the green line to be rotated from the vertical by $|\theta_0|$, where $s=R|\theta_0|$. The angle $\beta_0$ represents the net amount that the cylinder has rotated relative to the Earth frame (i.e., the amount by which the blue line has rotated CCW).

 

[CAF123]

Thanks TSny, the sketch was very clear. Did you get that the constraint was $R\alpha = \phi (r-R/2)?$_{(has no θ dependence?)}

When the cylinder is at the bottom and rotated CW, the point that was originally intersected by the vertical passing through the centre of the pipe is rotated by an angle θ, which creates an arc length Rθ. Another point on the cylinder has traveled the same distance since the cylinder does not slip, given by $r\phi$. If we now consider rotation of angle α of the pipe, then by looking at the sketch, $R\alpha = R\theta + R(\alpha - \theta) = R\theta + R(\phi/2)$. I got the second equality by geometry (via the triangles I was talking about earlier). Replace Rθ with $r\phi$.

 

[TSny]

$R\alpha = R\theta + R(\alpha - \theta) = R\theta + R(\phi/2)$. I got the second equality by geometry (via the triangles I was talking about earlier).

OK, I think I see why you are not getting $r$ anywhere in your expression. You are assuming $r = R/2$ since the figure in the problem appears to draw the diameter of the cylinder with a length that is close to the radius of the pipe. But, I don't think you want to make that assumption. The answer for T given in the problem does not make that assumption.

Otherwise, I agree with your relation. You just need to replace R/2 by r in the last term on the right of your equation quoted above..

 

[CAF123]

OK, I think I see why you are not getting $r$ anywhere in your expression. You are assuming $r = R/2$ since the figure in the problem appears to draw the diameter of the cylinder with a length that is close to the radius of the pipe. But, I don't think you want to make that assumption. The answer for T given in the problem does not make that assumption.

I did think that initially, but then given the fact that T had a term (R-r) for example, I dismissed the assumption. Where in my analysis do you think I assumed R/2=r? Do you agree that $\alpha - \theta = \phi/2$?
Thanks.

 

[TSny]

I did think that initially, but then given the fact that T had a term (R-r) for example, I dismissed the assumption. Where in my analysis do you think I assumed R/2=r?

I assumed you were taking r = R/2 when you wrote the term $R(\phi/2)$ in your equation for $R\alpha$.

Do you agree that $\alpha - \theta = \phi/2$?

No, I don't agree with this. My expression contains both $R$ and $r$. How did you get the 1/2 factor on the right side?

 

[CAF123]

I assumed you were taking r = R/2 when you wrote the term $R(\phi/2)$ in your equation for $R\alpha$.

Oh, I see. What I was actually doing was setting $\alpha-\theta=\phi/2$ and so in the term $R(\alpha-\theta)$, I made the sub and had $R(\phi/2)$.

No, I don't agree with this. My expression contains both $R$ and $r$. How did you get the 1/2 factor on the right side?

I 'derived' it from a series of geometric observations using the triangles I posted earlier. Here is what I did:
In the isosceles triangle, I have that $2x + \phi = \pi \Rightarrow x = (\pi-\phi)/2$. Then sum the angles along the radius of the pipe shown in the question (a portion of this radius is a side of the right angled triangle shown in the sketch). This gives $\pi = \pi /2 + x + λ$ which means $\lambda = \phi/2$.

Summing up the angles in this triangle now (the triangle where the symbol $\alpha$ is printed in the question) gives $\pi = \lambda + (\alpha - \theta) + p$, where $p = \pi - \phi$. Subbing in and solving gives $(\alpha - \theta) = \phi/2$.

Could you follow that? If so, does it make sense?

 

[TSny]

I'm sorry I can't follow this without a picture showing the specific triangles with which you are working. Any way you could attach one?

I don't see how your chord of the cylinder meets a radius of the pipe to form a right triangle. If you were to draw the cylinder with a considerably smaller radius r, would you still be able to construct your triangles?

 

[CAF123]

I don't see how your chord of the cylinder meets a radius of the pipe to form a right triangle.

You're right, it doesn't. Okay, so the reasoning is that since all angles are measured in the same sense and there is no slipping of surfaces, when a point on the pipe undergoes an angular displacement $R(\alpha-\theta)$, the same point on the rim of the cylinder undergoes an angular displacement $r\phi$?

The rest of the question was fine, thanks TSny.

 

[TSny]

You're right, it doesn't. Okay, so the reasoning is that since all angles are measured in the same sense and there is no slipping of surfaces, when a point on the pipe undergoes an angular displacement $R(\alpha-\theta)$, the same point on the rim of the cylinder undergoes an angular displacement $r\phi$?

Yes, the constraint is $r\phi = R(\alpha-\theta)$.