Cylindrical dowel pins are not completely rounded

[Juanda]

TL;DR Summary

I saw a video claiming that cylindrical dowel pins are not cylindrical but more like a trilobed shape. I'm trying to understand more about it.

I know there are no perfect things when it comes to manufacturing. And when precision is required, the smallest defect can be unacceptable.

I was watching this video about setting a mill up to spec and the author mentioned that dowel pins are not truly rounded so they shouldn't be treated as such for precision calibration of manufacturing tools. Instead, he recommends using proper gage pins which makes perfect sense. After all, that's what they have been made of.

What I don't understand is the explanation about the dowel pins. He actually gives an explanation with nice pictures included but I still don't understand it, probably due to the language barrier and my inexperience with machining.
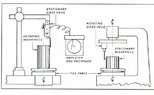
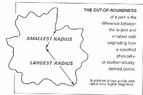
He claims that, since dowel pins are not grounded between centers, the resulting geometry will be something like this. I don't understand that claim. I tried googling it and asking for information in the YouTube message board but I still couldn't understand it.

What does grounding between centers even mean?


For context, this is the video in question. I have clipped it to start at the moment where he introduces this point although I consider the full video to be pretty interesting and entertaining.


Thanks in advance

 

[Lnewqban]

Please, see:
https://pmpaspeakingofprecision.com...-triangle-effect-pseudo-roundness-and-lobing/

https://en.wikipedia.org/wiki/Cylindrical_grinder#Centerless_grinding

 

[Ranger Mike]

Lobing errors are present on most all production parts. Takes high precision measurement to know truth.

 

[phinds]

If you buy wooden dowels at any hardware store that I am aware of, and certainly all of the many dozens I've bought over the years, they are to any reasonable degree of accuracy round, not trilobed. I certainly don't dispute that you CAN make them trilobed, but those in hardware stores are round. I suppose that a microscopic inspection might show slight out of round but to the degree needed in woodworking, that's irrelevant.

 

[Ranger Mike]

wood is not metal. You can not measure out of roundness in a diametric manner regardless of the material, wood, plastic, ceramic, steel.

 

[Juanda]

Please, see:
https://pmpaspeakingofprecision.com...-triangle-effect-pseudo-roundness-and-lobing/

https://en.wikipedia.org/wiki/Cylindrical_grinder#Centerless_grinding

Yes. That's exactly what I meant. But those sources still don't explain how that ends up happening. If it's possible to deduce it from the pictures and information given I couldn't put the pieces together myself.

 

[Juanda]

Lobing errors are present on most all production parts. Takes high precision measurement to know truth.

View attachment 351195

View attachment 351196

And I won't most likely need it in my engineering life. It seems this level of accuracy is only relevant when manufacturing the machines that will manufacture parts because errors there will end up in the manufactured parts too and they could accumulate.
I guess it'd also be necessary if you're manufacturing an extremely precise component but that's not been my field so far. At least not to the degree where I need to worry about how rounded the pins are.
Still, I find it a very curious phenomenon I still don't understand how ends up happening. I can't understand what's the driving mechanism causing that shape.

Here is an unrelated example to better explain myself. In roads, most debris ends up on the road shoulders. This initially seems to have no apparent reason because no one is pushing for that to be the case but it still happens that way. The underlying reason is a random walk of the debris as cars hit them until they reach a position where they are no longer hit which is the road shoulder.
In this case, I'm trying to understand the underlying cause behind this trilobed (or more odd number of lobes according to the article from @Lnewqban) shape. No one is trying to get this kind of shape but it still shows up when centerless grinding is used.

By the way, the pictures you showed are very illustrative and the explanation of them makes sense. But why that shape?
In colloquial language, I'd think nature tends to the simplest solutions which in this case would be a circle so that as the part rotates the cord length AB remains the same as explained in the picture you posted.
The fact that a constant-width shape that's not a circle comes up by itself is baffling to me. The mere existence of these shapes and how they roll without being circular makes me feel strange.

 

[Juanda]

If you buy wooden dowels at any hardware store that I am aware of, and certainly all of the many dozens I've bought over the years, they are to any reasonable degree of accuracy round, not trilobed. I certainly don't dispute that you CAN make them trilobed, but those in hardware stores are round. I suppose that a microscopic inspection might show slight out of round but to the degree needed in woodworking, that's irrelevant.

And I fully agree with you. My work isn't with wood but for me, dowel pins are still round enough.
However, the point isn't that we CAN make them trilobed. The strange thing is that the trilobed (or more odd number of lobes) shape shows up by itself due to the centerless grinding process to manufacture them.
I think it's incredibly strange and I'd like to understand it better.

 

[Juanda]

The mere existence of these shapes and how they roll without being circular makes me feel strange.

Not completely related to the post but as I talked about it I remembered a great couple of videos worth recommending.

 

[Ranger Mike]

I can take time to explain this whole thing but seems you do not need to know.
Short answer is three lobe parts come from parts made in 3 jaw chucks.
if you want more info, let me know,

 

[Juanda]

I can take time to explain this whole thing but seems you do not need to know.
Short answer is three lobe parts come from parts made in 3 jaw chucks.
if you want more info, let me know,

I do want more information. I understand that explaining it yourself can take time, so if you could direct me to other sources, I can read them and try to understand it myself.

Also, from your explanation, it seems that if the part was made on a 4 or 6-jaw chuck, that would determine the number of lobes. However, a previous article mentioned that they always come out with an odd number of lobes. So far, I have seen them with either 3 or 5 lobes.

I’m not sure if this is because jaw chucks always have an odd number of holding points or if it’s due to something else. The article pointed out that having an odd number is necessary so that the low and high spots cancel each other, ensuring a constant width.

 

[Ranger Mike]

Metrology is the Science of Measurement

Measurement is the language of Science

Measurement is a Universal Language


In any production endeavor, a standard must be met to provide the closest to practical same parts to the customer, time after time.
Ford Motor would not like a piston coming in 0.002" over size, let alone , 10,000 of them!

Hence, we have a Standard to determine proper specification.

As an aside, I have built many race car engines and never install parts out of the shipping carton. I measure them ALL, to see if they are in spec. Most are NOT.

In manufacturing of high production precision parts there are 3 things that must be in tolerance.

Size, Shape and Surface Texture ( bastardized to mean surface finish) in layman terms.

Size is a very loose spec. As this post reveals. Lobing conditions in the manufacturing process mean you will almost certainly have some form error. How much depends on the application. A wheel barrow bushing can have lots of out of roundness but who cares. A wheel bearing using a bushing is another matter. Next comes form error that requires a different measurement technique.

Out of roundness is defined ( by NIST) as the maximum radius minus the minimum radius and can not be measured with common shop floor gages. An example of form error is a fracking elbow suffering blow by at 15,000 psi pressure.

Was generated on a machining center and had 0.003" out of roundness. No wonder it has blow by.

Finally Surface texture requires expensive metrology instruments having diamond stylus contacts wired to electrics to show deviation to the millionth of an inch.

Henry Ford bought a Rolls Royce engine ( circa 1930s0 and had his engineers copy it. They did. Prototype blew up in an hour. They did not look at surface texture. The pistons were mirror smooth. Did not hold lubrication and boom. Chevy Vega sound familiar?

Now you know the Three Ss..Size, Shape , Surface texture of dimensional measurement.

Causes of Form Error - All surfaces of a typical OD are generated with reference to fixed points, axes or lines of contact in the machine tool, be it centerless grinding, lathe centers, steady rests, regulating wheels, tool edges, grinding wheel surfaces. These points of contact are constantly changing. Tool holders flex, there is imperfect rotation, erratic cutting dynamics, tooling wear, lubrication, rotational imbalance and wear, improper machine tool geometry, all contribute to error. Tool holders and holding fixtures slip, belts wear, drive rollers misalignment, chucks distort, localized heating, excessive feed rates, and warped out of round stock all add to the mix.

Finally, it seems that the most common machine tool used, “center-less” Machine tools were designed to make out of round parts! They contact the production part at three points and almost always generate a 3,5 or 7 lobe part.

It should be noted that one could not effectively measure SIZE of high precision parts without knowing the Shape …i.e. effects of form deviation due to lobbing error generated during the machining process.

Knowing Form Error is mandatory, when assembling tight tolerance precision parts. The time-honored mistake of “ tightening up the Tolerance” will not cure the problem. Control of Form Error will reduce scrap, reduce rework, eliminate waste and save time and money.

https://www.mmsonline.com/columns/approximating-geometry-measurement​

 

[Ranger Mike]

I do want more information. I understand that explaining it yourself can take time, so if you could direct me to other sources, I can read them and try to understand it myself.

Also, from your explanation, it seems that if the part was made on a 4 or 6-jaw chuck, that would determine the number of lobes. However, a previous article mentioned that they always come out with an odd number of lobes. So far, I have seen them with either 3 or 5 lobes.

I’m not sure if this is because jaw chucks always have an odd number of holding points or if it’s due to something else. The article pointed out that having an odd number is necessary so that the low and high spots cancel each other, ensuring a constant width.

four jaw chucks make even lobed parts

 

[Juanda]

Thank you for the insightful response @Ranger Mike. It's enlightening.

As an aside, I have built many race car engines and never install parts out of the shipping carton. I measure them ALL, to see if they are in spec. Most are NOT.

I feel you. I have encountered the same situation in my work, which drives me crazy.

Finally, it seems that the most common machine tool used, “center-less” Machine tools were designed to make out of round parts! They contact the production part at three points and almost always generate a 3,5 or 7 lobe part.

So it's been established this is a well-known phenomenon. Still, the main question remains. What's the driving force behind it causing those specific shapes? Yes, it's the imperfections in the manufacturing process but I find it so strange that those kinds of shapes appear by themselves.

four jaw chucks make even lobed parts

Are you sure about it? It feels impossible to have a constant width part with an even number of lobes.
In the previous article I discussed in mentioned they always come out with an odd number of lobes so the constant width remains. The picture you showed also imposes that the resulting shape must have constant width.
From wiki: https://en.wikipedia.org/wiki/Curve_of_constant_width

Every regular polygon with an odd number of sides gives rise to a curve of constant width, a Reuleaux polygon, formed from circular arcs centered at its vertices that pass through the two vertices farthest from the center. For instance, this construction generates a Reuleaux triangle from an equilateral triangle. Some irregular polygons also generate Reuleaux polygons.

As a counterexample, if it were even numbered, you would not be able to see a constant width across its perimeter. A diametrical measure would reveal differences. Sorry for the crude drawing but this is what I'm trying to say.

 

[Ranger Mike]

So it's been established this is a well-known phenomenon. Still, the main question remains. What's the driving force behind it causing those specific shapes? Yes, it's the imperfections in the manufacturing process but I find it so strange that those kinds of shapes appear by themselves.

This is the reality of the manufacturing world. These shapes exist. They must be understood and either corrected or their magnitude must be known.




A diametrical measure would reveal differences.
NO it would not.
Look at post 12 above. You can only check lobing condition if you are able to measure differences in the RADIUS, not the Diameter, these are two different measurements. You must re-read post 12 and understand.

The part must be placed on a precision rotary table and centered so the change in RADIUS can be measured, or the part is scanned on a high accuracy scanning CMM. we ate talking accurate to 100 millionths of an inch or better. .005 mm accuracy. In this way a center point is used as datum and the radius of the outside diameter can be measured.

 

[Juanda]

NO it would not.
Look at post 12 above. You can only check lobing condition if you are able to measure differences in the RADIUS, not the Diameter, these are two different measurements. You must re-read post 12 and understand.

The part must be placed on a precision rotary table and centered so the change in RADIUS can be measured, or the part is scanned on a high accuracy scanning CMM. we ate talking accurate to 100 millionths of an inch or better. .005 mm accuracy. In this way a center point is used as datum and the radius of the outside diameter can be measured.

I was referring to even-numbered lobed shapes. I said that because I believe that constant-width shapes can't have an even number of lobes. Does anybody know for sure if it's possible to have even-numbered lobed shapes with constant width? The wiki article I shared earlier focuses on odd numbers, which aligns with the explanation of low peaks and high peaks being opposed so that the diametrical measure remains consistent. Therefore, my crude drawing with 4 lobes was intended to show how this opposition is not possible when the number of lobes is even.

Still, I checked again post #12 as you said and looked into the link. I'm sorry I missed it but I thought the main information was in the picture and there were only odd numbered lobed shapes there.

Within the link you shared the following is said:

The condition is very common when using centerless grinding, but it is often not noticed because: 1) the part specs don’t call for any geometric analysis; and 2) the shop only uses a two-point dimensional gage, which is incapable of detecting the problem.

Understanding the geometry involved is the key. Out-of-roundness is either symmetrical, involving regular or geometrically arranged lobes or points on the part’s circumference, or asymmetrical, where the lobing is not regular. Most machining processes create symmetrical lobing, producing either an even or an odd number of lobes. Even-number lobing is sometimes seen in precision boring operations, caused by a worn or out-of-balance spindle. Odd-number lobing can be caused by a three-jaw chuck (producing a three-lobed workpiece) or a centerless grinder (which can also create a five-lobed condition). Asymmetrical lobing cannot be measured by the means described here, but it is evidenced by irregular travel of an indicator and usually indicates a problem in the tool.

I believe we're mixing concepts. We were discussing the lobed shapes caused by centerless grinding. If the previous picture from #3 is true, that would imply that only odd-number lobing is possible when the shape is obtained through centerless grinding. That is if we assume that constant width requires an odd number of lobes which I still don't know if it's true. I must say that the article seems to imply that it's possible for a constant-width shape to have an even number of lobes.

View attachment 351195

Even-number lobing appears when different manufacturing processes are used. An out-of-balance spindle combined with non-symmetric stiffness generating that kind of shape is something I can fit in my head.

However, how centerless grinding generates constant-width shapes instead of simple circles remains a mystery to me.

 

[Ranger Mike]

For the 3rd time, diameter checks do not see lobing errors. Your constant width fixation ignores what i have said. You can generate what you call constant width parts that still have lobing.
Wikipedia is not the end all source, especially in Metrology.

 

[Juanda]

For the 3rd time, diameter checks do not see lobing errors. Your constant width fixation ignores what i have said. You can generate what you call constant width parts that still have lobing.
Wikipedia is not the end all source, especially in Metrology.

I'm not particularly interested in diameter checks to see if there are lobes. My focus is on understanding how imposing constant width due to the manufacturing through centerless grinding results in odd-number lobed shapes that fulfill the constant width condition instead of simple circles which would also fulfill it.

Still, that doesn't change the fact that, if the shape doesn't have a constant width, diameter checks will definitely produce different readings depending on the rotation of the shaft. That's how constant width is defined after all. Isn't it?
And if that's true and we consider that only odd-number lobed shapes can have constant width, an even-number lobed shape could be revealed with diameter checks and discarded if necessary. That's what I tried to say with the tangential note that generated this side discussion.

 

[Ranger Mike]

That's how constant width is defined after all. Isn't it?
No it is not and how you decided to create some new metrology term is beyond me?

And if that's true and we consider that only odd-number lobed shapes can have constant width, an even-number lobed shape could be revealed with diameter checks and discarded if necessary.
It is not true.

 

[Juanda]

That's how constant width is defined after all. Isn't it?
No it is not and how you decided to create some new metrology term is beyond me?

I don't think I created a new metrology term. Constant width is a well-defined mathematical term to describe shapes that have a constant diameter along its perimeter.
https://en.wikipedia.org/wiki/Curve_of_constant_width

In geometry, a curve of constant width is a simple closed curve in the plane whose width (the distance between parallel supporting lines) is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler.[1] Standard examples are the circle and the Reuleaux triangle.

Even if the word constant-width is not a term directly often used in Metrology, it has an impact on it. Circle is also a word from Math and it impacts metrology as well.
More closely related to Metrology, I have seen constant-width being referred to as pseudo-roundness too with an equivalent description.
(Original link in post #2)

Pseudo-roundness is best defined as any shape not perfectly round, which exhibits constant dimensions when measured in any direction between two parallel planes, ie, with a 2 point micrometer.

In post #3 the picture mentions how the cutting points create a constant cord length between the points AB which I have interpreted as responsible for the resulting constant-width. I insist on the term constant-width because it's shown in other sources and also coincides with the odd-number lobed shapes shown as a result of centerless grinding.

Lobing errors are present on most all production parts. Takes high precision measurement to know truth.

View attachment 351195

And if that's true and we consider that only odd-number lobed shapes can have constant width, an even-number lobed shape could be revealed with diameter checks and discarded if necessary.
It is not true.

What isn't true? That constant width is only possible when there is an odd number of lobes?
I actually don't know it for sure and I'd love to see the proof as I asked for in a previous post.

I was referring to even-numbered lobed shapes. I said that because I believe that constant-width shapes can't have an even number of lobes. Does anybody know for sure if it's possible to have even-numbered lobed shapes with constant width?

All sources I could see about constant-width/pseudo-round shapes mention odd-number lobed shapes. Either in written form, drawn or hand-wavy explanations such as "the high spots have low spots opposite to it" which implies they must have an odd number of lobes. To me, the hand-wavy explanation I just gave (I saw it somewhere else) seems solid but I don't have a hard mathematical proof.
A simple counterexample of an even-number lobed shape being pseudo-round / having constant-width would be enough to refute it but I haven't found it yet.

 

[Ranger Mike]

My last attempt - You can have constant width in a tree lobe part and a 4 x class 5' diameter ring gage that is certifiable to 1 millionth of an inch. Both will indicate a constant width. When measured diametrically.
Both fill preform different in a application. One will have perfect sealing in pressure applications. One will have blow by and not seal due to form imperfections.

 

[Juanda]

My last attempt - You can have constant width in a tree lobe part and a 4 x class 5' diameter ring gage that is certifiable to 1 millionth of an inch. Both will indicate a constant width. When measured diametrically.
Both fill preform different in a application. One will have perfect sealing in pressure applications. One will have blow by and not seal due to form imperfections.

I'm sorry but I'm not sure I'm understanding the first part of the message.
You say you can have a three-lobe part and a what? I tried typing "4 x class 5' diameter ring gage" on the browser.

I think you're saying that both the male part and female hole, if having constant width, will produce the same measurement if their diameters are checked. Is that what you meant? I agree with that from the beginning.

And I agree with you in the second part of the message as well. The closer to a circle, the better seal will be obtained.
Having constant width isn't enough to guarantee proper seals because, although circles have constant width, not all constant-width shapes are circles.
Constant width means that a diameter measurement will always produce the same result no matter at which point it is measured. Alternative measure methodologies must be used to correctly describe the form as you stated before.
If the manufacturing process can only result in constant width shapes (centerless grinding), then the more lobes the better since it'll be closer to a circle.

I believe the point where we disagree is that I think constant width is only possible with an odd number of lobes and you disagree.
I insist, I'm not saying an even number of lobes isn't possible. We have discussed that already. I'm not even saying that an even number of lobes won't perform correctly. Since having more lobes could make it closer to a circle (depending on what we mean by a term as broad as "closer"), then it's possible it'd work better for seals even while lacking the constant-width property. I'm just saying I don't believe that'd be a constant-width shape.

Still, I don't consider that to be the main point of discussion of the thread anyway. As I stated in a previous post:

My focus is on understanding how imposing constant width due to the manufacturing through centerless grinding results in odd-number lobed shapes that fulfill the constant width condition instead of simple circles which would also fulfill it.

If the whole issue regarding the number of lobes and constant width is still unclear among us I'd try to open a separate thread in the math section of the forum to seek confirmation about it there. Someone might be familiar enough with these geometries to be able to verify it.

 

[Ranger Mike]

i am out of here