- #1
Juanda
Gold Member
- 426
- 138
- TL;DR Summary
- I saw a video claiming that cylindrical dowel pins are not cylindrical but more like a trilobed shape. I'm trying to understand more about it.
I know there are no perfect things when it comes to manufacturing. And when precision is required, the smallest defect can be unacceptable.
I was watching this video about setting a mill up to spec and the author mentioned that dowel pins are not truly rounded so they shouldn't be treated as such for precision calibration of manufacturing tools. Instead, he recommends using proper gage pins which makes perfect sense. After all, that's what they have been made of.
What I don't understand is the explanation about the dowel pins. He actually gives an explanation with nice pictures included but I still don't understand it, probably due to the language barrier and my inexperience with machining.
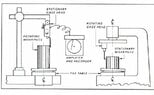
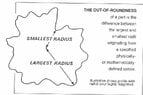
He claims that, since dowel pins are not grounded between centers, the resulting geometry will be something like this. I don't understand that claim. I tried googling it and asking for information in the YouTube message board but I still couldn't understand it.

What does grounding between centers even mean?
For context, this is the video in question. I have clipped it to start at the moment where he introduces this point although I consider the full video to be pretty interesting and entertaining.
Thanks in advance
I was watching this video about setting a mill up to spec and the author mentioned that dowel pins are not truly rounded so they shouldn't be treated as such for precision calibration of manufacturing tools. Instead, he recommends using proper gage pins which makes perfect sense. After all, that's what they have been made of.
What I don't understand is the explanation about the dowel pins. He actually gives an explanation with nice pictures included but I still don't understand it, probably due to the language barrier and my inexperience with machining.
He claims that, since dowel pins are not grounded between centers, the resulting geometry will be something like this. I don't understand that claim. I tried googling it and asking for information in the YouTube message board but I still couldn't understand it.
What does grounding between centers even mean?
For context, this is the video in question. I have clipped it to start at the moment where he introduces this point although I consider the full video to be pretty interesting and entertaining.
Thanks in advance