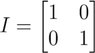Data from Normal D is Uncorrelated?

[WWGD]

Hi All, I am looking at the page http://www.visiondummy.com/2014/04/geometric-interpretation-covariance-matrix/

In which White Noise in 2D is defined as the/a graph of uncorrelated data, so that the associated co. It is sassociated covariance matrix is the identity. It is stated at one point that one such example is that of data drawn from a standard normal. Can anyone see why this is uncorrelated? Is it because the variance has been normalized to 0, or is there something else?

 

[andrewkirk]

I guess you're referring to the statements

Let’s start with unscaled (scale equals 1) and unrotated data. In statistics this is often referred to as ‘white data’ because its samples are drawn from a standard normal distribution and therefore correspond to white (uncorrelated) noise:
[Image]
The covariance matrix of this ‘white’ data equals the identity matrix, such that the variances and standard deviations equal 1 and the covariance equals zero

The data shown in the graph appears to be drawn from a bivariate normal with the identity matrix as covariance matrix, so that it has standard normal marginals and no correlation. The scatterplot is approximately circular, with no apparent trend, as is expected from uncorrelated variates.

I'm afraid I don't fully understand what your question is though.

 

[WWGD]

Ah, thanks, I had not seen the assumption in the link of the two variables being uncorrelated, so I did not know why the two were said to be uncorrelated.