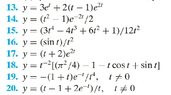karush
Gold Member
MHB
- 3,240
- 5
#19
$t^3y'+4t^2y=e^{-t},\quad y(-1)=1,\quad t>0$
rewrite
$y'+\dfrac{4}{t}y=\dfrac{e^{-t}}{t^3}$
$u(t)=e^{\int 4/t \, dt}=e^{4\ln \left|t\right|}=t^4$first bold steps...
typos?
$t^3y'+4t^2y=e^{-t},\quad y(-1)=1,\quad t>0$
rewrite
$y'+\dfrac{4}{t}y=\dfrac{e^{-t}}{t^3}$
$u(t)=e^{\int 4/t \, dt}=e^{4\ln \left|t\right|}=t^4$first bold steps...
typos?