De Moivre's theorem to express power

Join the discussion

Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.

Real named experts · corrections over time · the nuance an AI answer skips

1 reply · 1K views

lee123456789

Homework Statement: <Moderator's note: Please fill the Homework Statement correctly>

Relevant Equations: <Moderator's note: Please fill the Relevant equations correctly>

A)Use de moivres therom to express power in simplest polar form

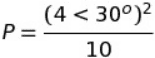
Workings

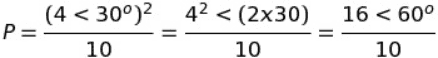
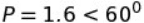Do i need to divde the 60^o by 10 aswell

Physics news on Phys.org

Babadag

If P=4*[cos(30o)+i*sin(30o)] then P^2/10=1.6*[cos(60o)+i*sin(60o)]

So, you don't need to divide then the final argument also[60o].

Similar threads