Decompose the E field into conservative and non-conservative parts

[alan123hk]

Recently, I've seen several discussion threads here about splitting electric fields. I want to express my opinion. Of course, this is just a calculation method, not a basic physical concept, but it is also useful in some cases, at least not wrong.

The following is an example of the out of a transformer, which also implies the concept of splitting the E field.

​

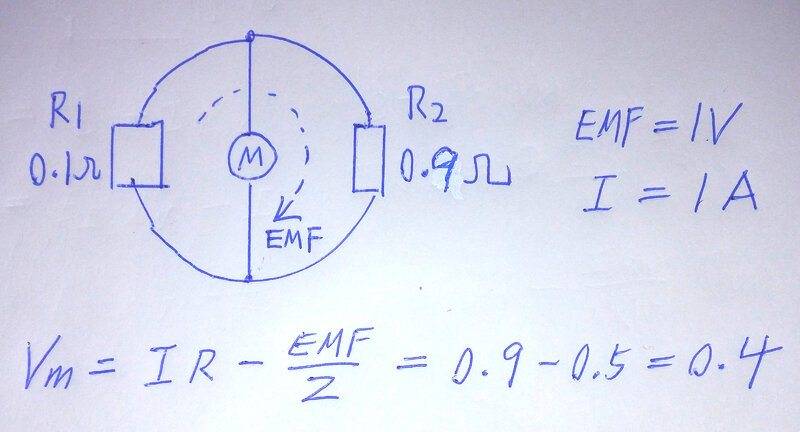
The following is a more practical example, assuming that the operating frequency is very low, and the magnetic field in the external space and wires is zero, how to find the displayed value of the voltmeter?
We can write down the voltage loop equations for the left and right sides and solve them. After a long and laborious process of derivation on at least one A4 sheet, I finally came to conclusion $~V_m=\frac{EMF}{2}\frac{R_2-R_1}{R2+R1}=0.4V~$, but using the concept of splitting electric fields gave immediate results.

​

It can also be used to evaluate the distribution of charges on the circuit, which is very interesting and practical, such as the following example, I believe it is not far from reality.

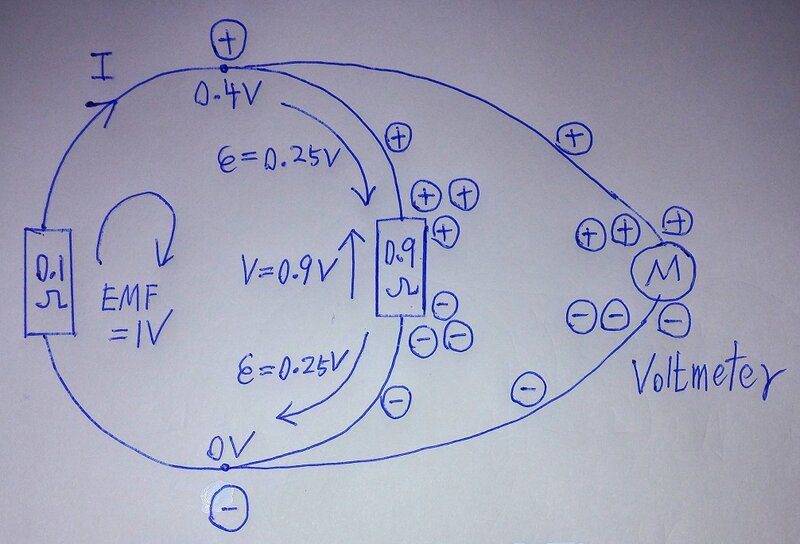
Please note that from the bottom 0V to the top 0.4V can be expressed as $~-0.25+0.9+-0.25=0.4V$
​

Sorry, I can only think of these few examples for now.

 

[SDL]

the magnetic field in the external space and wires is zero

If you assume this (at least no time-varying magnetic field in the external space), then the lumped element model is valid and all EMFs in the circuit are produced by only potential electric fields so you don't need to "split" anything. If an electric field is potential, then you are legal to introduce a potential function, so every node in your circuit will be assigned a scalar value. Sum of potential differencies (i.e. voltage drops) around every closed loop in the circuit equals to zero. This is exactly what Kirchhoff's Voltage Law states.

 

[SDL]

View attachment 317944

In this diagram, the source of "EMF=1V" is undefined. If lumped element model is valid here, then you have to add a power source with voltage drop on its terminals - a battary or an inductor. But if your EM system cannot be modelled with lumped elements, then all potentials at nodes (0V, 0.4V) are just invalid.

 

[alan123hk]

If you assume this (at least no time-varying magnetic field in the external space), then the lumped element model is valid and all EMFs in the circuit are produced by only potential electric fields so you don't need to "split" anything. If an electric field is potential, then you are legal to introduce a potential function, so every node in your circuit will be assigned a scalar value. Sum of potential differencies (i.e. voltage drops) around every closed loop in the circuit equals to zero. This is exactly what Kirchhoff's Voltage Law states.

I mean of course assuming no changing magnetic field in the external space.
I don't have to use splitting electric field, but the calculation will be much simpler and faster when I use it. I have already stated this and I think that the equation I gave has used the concept of splitting electric field, don't you agree ?

 

[SDL]

this is just a calculation method

Any calculation method is developed to simplify solving, not to obfuscate. In case of an inductor, first, the compensating external EMF of the potential electric field (which is actually a voltage drop across its terminals) and the induced EMF (by Faraday's law) have opposite directions. One would have to take this into account every time to not make mistakes. Second, the EMF induced by the time-varying magnetic field in the inductor is "hidden" inside the inductor in this model. For a circuit engineer, the inductor function is expressed just as v = Ldi/dt for its two point terminals and this is sufficient for him to solve circuits. The same is true for battaries - we don't care of any non-potential chemical forces inside that produce EMF and a voltage drop at battary's terminals.

 

[alan123hk]

In this diagram, the source of "EMF=1V" is undefined. If lumped element model is valid here, then you have to add a power source with voltage drop on its terminals - a battary or an inductor. But if your EM system cannot be modelled with lumped elements, then all potentials at nodes (0V, 0.4V) are just invalid.

This is a sketch related to the Lewin circuit paradox, if you are not familiar with this topic, it is really hard to know what I want to express, please refer to this link http://kirkmcd.princeton.edu/examples/lewin.pdf.

Any calculation method is developed to simplify solving, not to obfuscate

I think for people who understand this concept and can use it correctly, this calculation method is actually very simple, clear and reasonable.

 

[SDL]

This is a sketch related to the Lewin circuit paradox, if you are not familiar with this topic, it is really hard to know what I want to express, please refer to this link http://kirkmcd.princeton.edu/examples/lewin.pdf.

If you're talking about that "paradox", really it's not a paradox at all. There's a thread at this forum about it, I've just responded there: https://www.physicsforums.com/threads/lewins-circuit-paradox.1047023. Those all seem to be a paradox when the lumped model is incorrectly used or just inapppropriate. If you are still uncertain about any example circuit, please feel free to show it here and ask.

 

[alan123hk]

f you're talking about that "paradox", really it's not a paradox at all. There's a thread at this forum about it

I also mentioned in another discussion thread that there is actually no contradiction. What I want to discuss here is how to use the concept and method of splitting field. Since you said you couldn't understand my sketch, I suggest you refer to that link.

 

[SDL]

Ok, if you are trying to offer a new calculation method, we expect that it would not be just a simple one, it should be simplier than other methods, well khown and commonly used. First, you have provided a solution with three illustrations while only one is sufficient to solve the circuit. Second, on the 3rd diagram I can see an arrow directed CW with EMF=1V. My first question is "Where is it from?" I guess you would answer: "Look at the two previous pictures". We can see that this all is not simplification, but complication.

 

[vanhees71]

There is one and only one electromagnetic field. As any field in 3D Euclidean space both the electric and the magnetic components, which both form a vector and an axial-vector field, respectively, can be split in a rotation-free (conservative) and a solenoidal part. The magnetic field is a pure solenoidal field due to Gauss's Law,
$$\vec{\nabla} \cdot \vec{B} =0.$$
That's why, at least locally in simply connected regions of space, it can be written in terms of a vector potential,
$$\vec{B}=\vec{\nabla} \times \vec{A}, \qquad (1)$$
and any vector potential, which differs from $\vec{A}$ by
$$\vec{A}'=\vec{A}-\vec{\nabla} \chi \qquad (2)$$
describes the same $\vec{B}$. That's why $\vec{A}$ is an auxilliary field and is not directly observable.

For the electric field we have the constraint from Faraday's Law (in SI units),
$$\vec{\nabla} \times \vec{E} + \partial_t \vec{B}=0.$$
Because of (1) we have
$$\vec{\nabla} \times (\vec{E}+\partial_t \vec{A})=0.$$
This means that the field in the brackets is conservative (at least locally in simply-connected regions), i.e., we can introduce also a scalar potential,
$$\vec{E}+\partial_t \vec{A}=-\vec{\nabla} \Phi$$
or
$$\vec{E}=-\partial_t \vec{A}-\vec{\nabla} \Phi. \qquad (3)$$
Changing the "gauge" via (2) then needs also a change of $\Phi$, so that also $\vec{E}$ stays unchanged:
$$\vec{E}=-\partial_t \vec{A}' -\vec{\nabla}(\Phi+\partial_t \chi),$$
i.e., you have to set
$$\Phi'=\Phi+\partial_t \chi \qquad (4)$$
to get again
$$\vec{E}=-\partial_t \vec{A}' -\vec{\nabla} \Phi'. \qquad (5)$$
So the potentials $\Phi$ and $\vec{A}$ are both only determined up to a gauge transformation given by (2) and (4), and these are thus both not observable in principle.

The potentials can be determined by the inhomogeneous Maxwell equations, and you always have the freedom to choose some constraint to "fix the gauge", but that's another story. This shows that the split of $\vec{E}$ in a conservative and solenoidal piece is not as helpful as the expression in terms of the potentials $\Phi$ and $\vec{A}$.

The reason for this alternative split according to the potentials is, of course, that the mathematically more adequate point of view is that it's not only a field theory in Euclidean 3-space but also a relativistic QFT in 4D Minkowski space, and for the dynamics it's much more natural to work with the potentials than with the split according to Helmholtz's fundamental theorem in 3D.

 

[hutchphd]

I think for people who understand this concept and can use it correctly, this calculation method is actually very simple, clear and reasonable.

Epicycles and more epicycles.

 

[alan123hk]

Ok, if you are trying to offer a new calculation method, we expect that it would not be just a simple one, it should be simplier than other methods, well khown and commonly used

I did not say to provide a new calculation method, It would be great if I really have this ability. Of course, this method is not new, and if you search the Internet, there will be a lot of relevant information. As for whether it is widely known and accepted, I don't know.

on the 3rd diagram I can see an arrow directed CW with EMF=1V. My first question is "Where is it from?"

This EMF comes from a solenoid magnet in the center of the ring circuit, creating a time-varying circular area magnetic field. According to Faraday's law, the induced EMF on this circular circuit loop is 1V. If you've seen the link I suggested, you should know.

 

[SDL]

all potentials at nodes (0V, 0.4V) are just invalid

Please consider the followng very important fact. A vector calculus theorem says that if $\oint\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}=0$ along every closed path, then there exists a scalar function (potential) $\Phi$ such that $\mathbf{\vec{E}}=-\vec{\nabla} \Phi$. This is equivalent to independance of $\int_A^B\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}$ from a path from A to B, and we define this integral as "voltage drop": $V_{AB}=\int_A^B\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}=\Phi_A-\Phi_B$.

If this condition is false, then no such function exists, $\int_A^B\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}$ depends on a path from A to B, and all node potentials you've written just loose any meaning.

And be careful, an assumption "variable magnetic field in the external space and wires is zero" means that there are no solenoidal electric field outside. In your case, this is not true. So you cannot use any "potentials" and "voltage drops".

 

[SDL]

please refer to this link http://kirkmcd.princeton.edu/examples/lewin.pdf.

I've read this paper through and found no paradox there. Again, he tries to analyse the circuit using node potentials and voltage drops. Since the electric field in all the space around the area containing magnetic field is non-conservative, voltmeter readings would be different depending on voltmeter location, wire paths etc.

If you try to analyse such circuits using KVL plus some "lifehacks", you'd likely get incorrect results. Remember, $\int_A^B\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}$ depends on a path from A to B, and you'll need to care of location, geometry and paths of all elements and wires in a circuit subloop of interest. It is a numerical EM solver that would get it done correctly.

 

[alan123hk]

If this condition is false, then no such function exists, ∫ABE→⋅dl→ depends on a path from A to B, and all node potentials you've written just loose any meaning.

Of course, there is also a scalar function (potential Field), here we are talking about decomposing the electric field into two parts: the conservative field and the non-conservative field. The method I am using now is to find the voltage (potential difference) generated by the charges accumulated in the circuit, so I believe it can actually be used to find the part of the non-conservative electric field.

And be careful, an assumption "variable magnetic field in the external space and wires is zero" means that there are no solenoidal electric field outside. In your case, this is not true. So you cannot use any "potentials" and "voltage drops".

Of course, there is an induced electric field in the outer space away from the solenoid magnet. Theoretically, this induced electric field can extend to infinity, and if I recall correctly, in the space outside the area of the solenoid magnet, the electric field become conservative in one special case.

As a reminder, ignore possible time-varying magnetic fields in space outside the region of the solenoid magnet.

 

[SDL]

electric field will become conservative in space outside the area of the solenoid magnet.

No, it's a common illusion:

if $\oint\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}=0$ along every closed path

Don't forget topology. $\nabla\times\vec{E}=0$ in the space outside means only $\oint\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}=0$ along any closed path located fully outside, i.e. not surrounding a time-varying magnetic field. But if another path encircles the magnetic flux, this line integral becomes non-zero. In these cases, no potential function exists again, because it can be defined for the whole space only.
To summarize, an electric field can be conservative either everywhere or nowhere.

 

[alan123hk]

I misremembered, it seems like it only becomes a conservative field in one special case (post description corrected) That is to say, it is not applicable in the whole space.

 

[SDL]

As perfectly explained above by @vanhees71, there's only one electric field observable, but due to the theorem it can be split into conservative and solenoidal parts.
I guess you're trying to deal with the solenoidal part only since the conservative one is ok with its potential function. Actually this split doesn't make sense, because for a solenoidal E when calculating $\int_A^B\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}$ (in event of absence of convinient potentials) you'll likely fail. Indeed, having fixed all elements and the voltmeter in place, try to move any wire aside by a couple of inches and your voltmeter readings will immediately change.

 

[alan123hk]

As I said, I'm calculating the potential difference and the electric field due to the accumulated charge only, so of course the closed loop integral of the electric field due to the accumulated charge alone is zero.

If the position changes (move the wire, etc.), the charge distribution will of course change, and therefore the potential, but a conservative field will still be produced.

 

[SDL]

due to the accumulated charge only

That's the question! How do you calculate this charge distribution? Your EM system, unlike a lumped inductor, is not solid. After changing your loop geometry you'll get a different result! Of course the solution for a given geometry is valid, but what's the value of it? For example, if you design a microstrip structure, an EM solver would give you a perfect solution. But such structures are manufactured on PCBs and solid during their lifetime. But your circuit is assembled of resistors and wires and I guess is not solid.

 

[SDL]

Having disassembled a factory inductor or transformer you would be able to observe all the effects discussed above - a solenoidal electric field, a complex charge distribution compensating that field along the wire etc. And if you stretch it or deform in some other way, its properties certainly change. Google for formulas for inductor designers and you'll see that they all contain geometrical variables. But circuits are represented as graphs, which define only connections of solid elements, but not circuit geometry. That's the main difference.

 

[alan123hk]

That's the question! How do you calculate this charge distribution?

Of course, calculating the charge distribution is much more complicated and may require computer simulations. What we can discuss here is how to calculate the potential difference. If we know the potentials at all points on the circuit, then theoretically we can calculate the associated conservative electric field, and finally the charge distribution on the circuit can be determined accordingly.
This so-called "split electric field" approach is only one option. As in the example I provided here, I can use another method (whether we call it Split Fields or not) to calculate the potential difference between two points in any part of the ring circuit. The trick is to find a general formula that works for any shape first, so it's much easier to calculate later. This also explains why there is a weird down arrow labeled 0.25V in my previous diagram.

 

[SDL]

First, one has to agree that your examples do not belong to those the circuit theory deals with, because KVL is not true here. Despite of it they can be modelled with lumped elements. I suppose you have been inspired by that paper about a circuit paradox or maybe by some discussions at other threads/forums. A circuit with a localized magnetic flux inside is a very special case emloyed to offer that "paradox" to public. Please explain why to continue putting effort to develop analysis of this kind of EM systems? Do you see any practical usage or just academic interest? No, I'm not going to discourage you, just want to know.

 

[alan123hk]

You said that this circuit does not comply with KVLl, I respect your opinion. But I think I'm using KVL to analyze it.
Whether I'm particularly interested in this circuit is beside the point. I use this circuit as an example to illustrate the application of "split Electric fields". I don't understand why many people think this method is unnecessary or not useful. I think that "split Eletric field" means considering that the electric field is a combination of two different fields Ev and Ea, and use it to help solve problems when need.

Does the article in this http://kirkmcd.princeton.edu/examples/lewin.pdf also mention using KVL and splitting E into Ev and Ea to handle the problem? Maybe it is unnecessary in advanced math models, but I think it can be useful in practice, at least for those who are not good at advanced math.

 

[SDL]

You said that this circuit does not comply with KVLl, I respect your opinion. But I think I'm using KVL to analyze it.

This is because the line integral of E along a closed path around the magnetic flux in this circuit is non-zero, while due to KVL it is zero. Certainly I mean the resulting E-field ("non-split").

It can also be used to evaluate the distribution of charges on the circuit, which is very interesting and practical, such as the following example, I believe it is not far from reality.

View attachment 317944​

On this diagram, there are two EMFs along two wires $\epsilon=0.25V$ each. For a perfectly conducting wire, if it neither accumulates/distributes nor dissipates energy, $\int_A^B\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}=0$ where A and B are its ends. On the other side, if you "split" the resulting field, $0=\int_A^B\mathbf{\vec{E}}\cdot \mathbf{\vec{dl}}=\int_A^B\mathbf{\vec{E_c}}\cdot \mathbf{\vec{dl}}+\int_A^B\mathbf{\vec{E_s}}\cdot \mathbf{\vec{dl}}$. So in order to calculate voltage drop $V_{AB}=\int_A^B\mathbf{\vec{E_c}}\cdot \mathbf{\vec{dl}}$ you need to calculate $\int_A^B\mathbf{\vec{E_s}}\cdot \mathbf{\vec{dl}}$ for the solenoidal part, which depends on path from A to B, i.e. on wire geometry.
Please argue how do you calculate $\epsilon=0.25V$ for either wire? Why not $\epsilon_1=0.3V$ and $\epsilon_2=0.2V$? What's the reason for them to be equal? Their sum is $\epsilon_1+\epsilon_2=0.5V$ in both cases, so not breaking the total EMF=1V.

 

[alan123hk]

Please argue how do you calculate ϵ=0.25V for either wire? Why not ϵ1=0.3V and ϵ2=0.2V? What's the reason for them to be equal? Their sum is ϵ1+ϵ2=0.5V in both cases, so not breaking the total EMF=1V.

This is a logical reasoning process.
Since the EMF for the entire loop is 1V, the EMF for a quarter of the loop length is 0.25V. Since the charge accumulating on the surface of the wire must produce the same Ec to cancel out Es to make the total E inside the wire zero, the corresponding potential difference over the length of this loop is also 0.25V.

So I don't actually need to use such a complicated calculation method to find 0.25V in post 22. But we can also use it as a validation method.

 

[SDL]

If we subtract the solenoidal part, the conserative remainder would have well-observed voltage drops.
The language of physics is mathematics and we all should speak it. Otherwise we take risks to get fantastic results. Under certain boundary and initial conditions Maxwell's equations have a unique solution. In order to scientifically prove your method you'll have to provide calculations.

 

[alan123hk]

First of all, I calculated the same result with Faraday's law, which is a kind of verification.
And that's exactly the same as the output of the transformer. Who would doubt that the voltage generated by the accumulated charge at the output of a transformer will be different from the induced EMF of the internal winding? And sometimes it is not easy to require strict mathematical proofs, so we can only resort to experimental proofs.

But since you say so, I'll give it a try. But this is not a strictly mathematical proof, just a statement of some facts. I hope I haven't made a mistake or misunderstood you.

​

After the charge accumulated on the surface of the wire cancels the induced electric field inside the wire, it will not weaken the potential difference it exhibits to the outer space

 

[SDL]

What I asked you to prove is why the EMFs along the two wires are the same and equal to 0.25V. That is to provide calculations instead of "locical reasoning". Can you solve your own circuit using EM laws?

 

[alan123hk]

What I asked you to prove is why the EMFs along the two wires are the same and equal to 0.25V. That is to provide calculations instead of "locical reasoning". Can you solve your own circuit using EM laws?

I really don't understand why you ask that.
As mentioned at the beginning, the center of the ring circuit has a circular area of varying magnetic field. According to Faraday's law of induction and the principle of symmetry, the induced electric field is a circular closed-loop electric field, and the field strength of any point in the loop is the same. Therefore, the electromotive force generated by any section on the circumference of the ring circuit is exactly equal to the constant Es multiplied by its arc length. Since the EMF of the entire ring circuit is defined as 1V, the EMF per quarter of the arc length is 0.25V.

This is because the line integral of E along a closed path around the magnetic flux in this circuit is non-zero, while due to KVL it is zero. Certainly I mean the resulting E-field ("non-split").

In fact, it is not difficult at all to make the closed-loop integral of the electric field in this AC circuit full of electromagnetic induction zero. Just replace the two resistors with two inductors. Since all wires in a circuit are perfect conductors with zero internal electric field strength, the closed loop integral must be zero. But the current of this circuit will not be infinite, because the alternating current is limited by the inductance. So is this circuit suitable for applying KVL now?

 

[alan123hk]

I suggest you take a look at this video. This may make you more familiar with this interesting story that started many years ago.

 

[SDL]

EMF per quarter of the arc length

On your diagram, I'd call this into question:

The EMF is proportional to the angle (this is to be proven separately). As shown on the picture above, angle $\varphi$ is less than $\pi/2$, so $\epsilon<0.25V$.
This is what I was talking about: The solution does depend on geometry, lumped elements' dimensions now matter. You have provided numerical results without giving exact problem conditions. And I asked you to argue them.

 

[alan123hk]

Since I marked both top and bottom as 0.25V, this already shows that the length of the resistor is assumed to be infinitely small, and the electric field inside the resistor becomes infinite, but the voltage of the resistor is still a fixed value. If I draw that resistor too small, it will be hard for people to see it.

In the example below, we can write the instant result 0.2V without solving complex voltage loop equations.

Is there any other way to find the answer so quickly without using the SPLIT FIELDS method?

​

 

[vanhees71]

I don't know, how you come to take two points and put some voltage on in it in a situation, where you have an EMF due to to a time-varying magnetic field. Due to Faraday's Law,
$$\vec{\nabla} \times \vec{E}=-\partial_t \vec{B}$$
there's no scalar potential for $\vec{E}$, and the EMF between two points depends on how you measure it. That's well demonstrated in this (in)famous lecture by Lewin quoted somewhere above, if I remember right. All you can say is that
$$\int_C \mathrm{d} \vec{r} \cdot \vec{E}=-\dot{\Phi}=1 \text{V},$$
where $\Phi$ is the magnetic flux through an arbitrary surface with boundary $C$. Choosing $C$ to run "along the circuit" the conclusion is that there is a current $i$ and Faraday's Law then tells you that $I=1 \text{V}/[(0.1+0.9) \Omega]=1 \text{A}$. Which voltages you measure between any two points "on the circuit" depends on the wiring of the voltmeter you attach to the two points!

 

[SDL]

Which voltages you measure between any two points "on the circuit" depends on the wiring of the voltmeter you attach to the two points

This is what I've been trying to express all the thread long.
As far as I understand the idea, he tries to decompose the resulting E-field into the solenoidal one having a constant value along a circle arond the flux (due to symmetry) and the conservative one, produced by induced charges, to finally satisfy Ohm's law along resistors and perfectly conducting wires.

It's possible to do that, but I can't still catch why. Your solution above for the loop current (and hence the EMFs along the two resistots) is straightforward.