Decomposing SU(4) into SU(3) x U(1)

[RicardoMP]

I'm solving these problems concerning the SU(4) group and I've reached the point where I have determined the Cartan matrix of SU(4), its inverse and the weight schemes for (1 0 0) and (0 1 0) highest weight states.

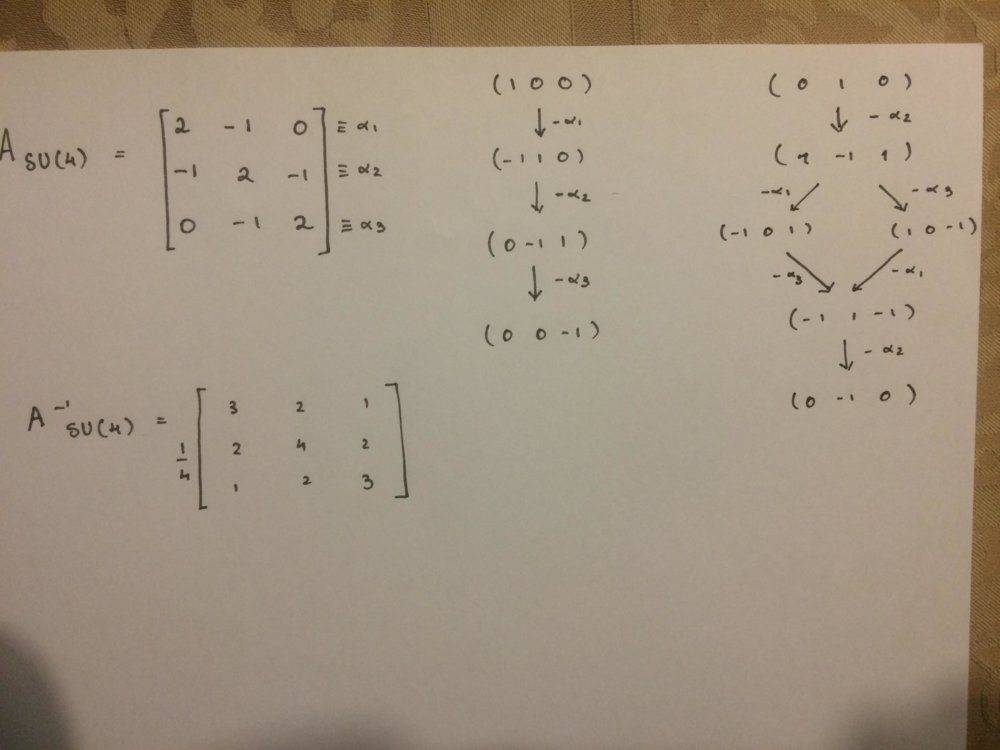
How do I decompose the (1 0 0) and (0 1 0) into irreps of SU(3) x U(1) using the inverse of the Cartan matrix of SU(4) and the weight scheme?

 

[fresh_42]

Can you elaborate who $SU(4)$ is connected to $SU(3) \times U(1)$? The dimension of $SU(n)$ is $n^2-1$ and the dimension of $U(n)$ is $n^2$. Hence we have $15$ on one side and $9$ on the other.

I only know the irreducible representations of $\mathfrak{su}(2)$, so I'm not sure what the classification theorem for $\mathfrak{su}(4)$ and $\mathfrak{su}(3)$ says. Not to mention the groups.