Mishal0488
- 20
- 1
- TL;DR Summary
- How does one model a spring mass system where the mass can disconnect with the spring and reconnect
Hi guys
Please refer to the attached image.
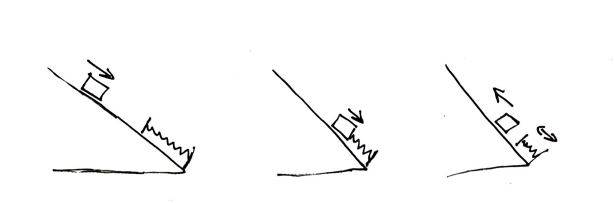
It is really easy to derive a set of differential equations which present a spring on a mass system, however how can one consider a system where the mass and spring can decouple? The first image on the left shows a spring a rest with a mass which is sliding closer to it. The middle image presents the same system but the spring and mass are now interacting with each other and the last image shows the case where the conditions of the system have caused the mass to move away from the spring and spring is still in motion until damping puts it to rest or the mass collides with the spring again...
How can one present such a system mathematically?
My only thought is to have several differential equations for each scenario and based on certain criteria only consider a specific set of differential equations to present the behavior. When changing between equations one would need to use initial conditions based on the past event. I am amusing that the system can be developed far more elegantly.
Any suggestions?
Please refer to the attached image.
It is really easy to derive a set of differential equations which present a spring on a mass system, however how can one consider a system where the mass and spring can decouple? The first image on the left shows a spring a rest with a mass which is sliding closer to it. The middle image presents the same system but the spring and mass are now interacting with each other and the last image shows the case where the conditions of the system have caused the mass to move away from the spring and spring is still in motion until damping puts it to rest or the mass collides with the spring again...
How can one present such a system mathematically?
My only thought is to have several differential equations for each scenario and based on certain criteria only consider a specific set of differential equations to present the behavior. When changing between equations one would need to use initial conditions based on the past event. I am amusing that the system can be developed far more elegantly.
Any suggestions?
Last edited by a moderator: