Darshit Sharma
- 100
- 13
- Homework Statement
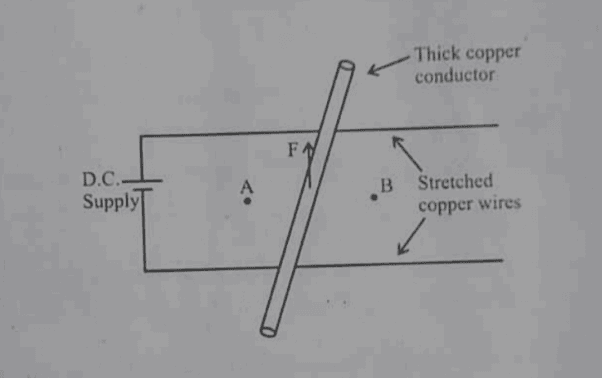
- Magnetic poles at the points A and B lying on either side of the conductor to experience the force in the upward direction
- Relevant Equations
- Flemming's left hand rule and Right hand thumb rule
As shown in the diagram, a copper conductor is placed over two stretched copper wires whose ends are connected to a D.C. supply. What should be the magnetic poles at points A and B lying on either side of the conductor to experience the force in the upward direction?----------
 ----------
----------
My understanding was that I tried to use Flemming's left-hand rule to figure out the polarity at the points. I followed the common manoeuvre which is as follows: I placed my central finger along the flow of current through the conductor and my thumb along the indicated force vector. A bit of confusion arose from here that the finger was just pointing from A to B so I used some of my understanding and concluded since the finger points towards B it may be as though the field lines were entering from below B and coming out of B i.e. perpendicular to the plane of the paper on which this dia is drawn. Since we see field lines coming out of that point I concluded that that point is the North pole and A is south.
Another thing was since the current flowed in a clockwise loop made with the conductor thus the pole at A must be south hence at B automatically north pole.
So after these two considerations, I concluded that the poles at A and B are the south and the north poles respectively.----------
This question was a test question in CISCE'S ICSE examination which we high schoolers give in India. (Grade 10).
However, the board didn't release an answer key this year.
And I had a cheap third-party answer booklet which just merely stated that the poles at A and B just need to be different not just specifically south and north.
Thus, the condensation is I wanted to ascertain whether my answer was right or not.
I want to understand the correct method by which the question can be solved, rather than my own pretty stupid method.
A better straightforward solution is anticipated.
Moreover, if anyone could instruct me where I lacked in the solution. Or if you notice any loopholes in my understanding.
(I ain't much confident though; I think I got this one wrong too)
Any help is appreciated.
My understanding was that I tried to use Flemming's left-hand rule to figure out the polarity at the points. I followed the common manoeuvre which is as follows: I placed my central finger along the flow of current through the conductor and my thumb along the indicated force vector. A bit of confusion arose from here that the finger was just pointing from A to B so I used some of my understanding and concluded since the finger points towards B it may be as though the field lines were entering from below B and coming out of B i.e. perpendicular to the plane of the paper on which this dia is drawn. Since we see field lines coming out of that point I concluded that that point is the North pole and A is south.
Another thing was since the current flowed in a clockwise loop made with the conductor thus the pole at A must be south hence at B automatically north pole.
So after these two considerations, I concluded that the poles at A and B are the south and the north poles respectively.----------
This question was a test question in CISCE'S ICSE examination which we high schoolers give in India. (Grade 10).
However, the board didn't release an answer key this year.
And I had a cheap third-party answer booklet which just merely stated that the poles at A and B just need to be different not just specifically south and north.
Thus, the condensation is I wanted to ascertain whether my answer was right or not.
I want to understand the correct method by which the question can be solved, rather than my own pretty stupid method.
A better straightforward solution is anticipated.
Moreover, if anyone could instruct me where I lacked in the solution. Or if you notice any loopholes in my understanding.
(I ain't much confident though; I think I got this one wrong too)
Any help is appreciated.
