Deep Learning the new key to nonlinear PDEs?

[BWV]

This paper getting some press, with promises that NNs can crack Navier-Stokes solutions more efficiently than traditional numerical methods.

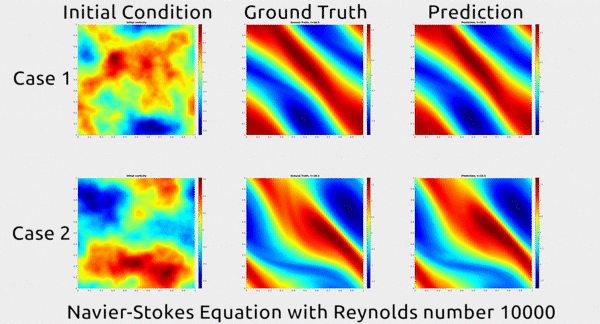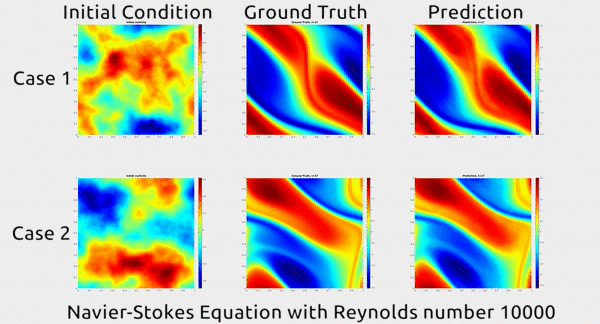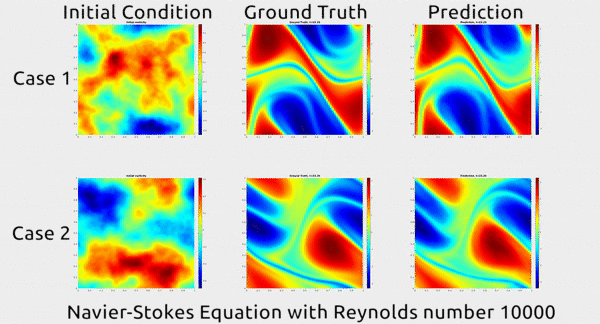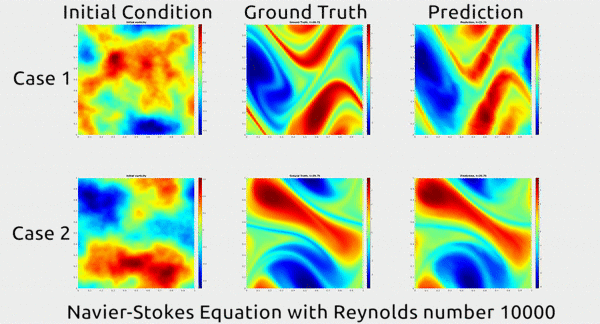
Now researchers at Caltech have introduced a new deep-learning technique for solving PDEs that is dramatically more accurate than deep-learning methods developed previously. It’s also much more generalizable, capable of solving entire families of PDEs—such as the Navier-Stokes equation for any type of fluid—without needing retraining. Finally, it is 1,000 times faster than traditional mathematical formulas, which would ease our reliance on supercomputers and increase our computational capacity to model even bigger problems
... In the gif below, you can see an impressive demonstration. The first column shows two snapshots of a fluid’s motion; the second shows how the fluid continued to move in real life; and the third shows how the neural network predicted the fluid would move. It basically looks identical to the second.

https://www.technologyreview.com/20...er-stokes-and-partial-differential-equations/

https://arxiv.org/abs/2010.08895

 

[Jarvis323]

There are some caveats and problems with the evaluation in the paper. I have to say I am pretty skeptical.

1) Performance testing compared with traditional solvers is not described in enough detail to understand the significance of the reported results. In fact there is only one sentence reporting a comparison, and it gives only a single data point.

In a sharp contrast, FNO takes 0.005s to evaluate a single instances while the traditional solver, after being optimized to use the largest possible internal time-step which does not lead to blow-up, takes 2.2s.

It is reported that both methods use the GPU, but it isn't reported which variation of a traditional method is used (there are a lot of strategies and variations), and there is no indication, or argument that the traditional method they chose is state of the art. Furthermore, they gave no details about how the computation was performed on the GPU, how the program was compiled, etc. They could easily have compiled their method with optimizations and the other without, or ran the them on different machines, or with carefully selected work sizes, or whatever to get the results they wanted, and they would not even be lying in the paper. They just omit all of these details.

2) The neural network must be trained before it can be applied. They report that training takes about 12 hours, which is still faster overall.

This amounts to 2.5 minutes for the MCMC using FNO and over 18 hours for the traditional solver. Even if we account for data generationand training time (offline steps) which take 12 hours, using FNO is still faster! Once trained, FNO canbe used to quickly perform multiple MCMC runs for different initial conditions and observations, while thetraditional solver will take 18 hours for every instance.

Supposing that this is true, and a good representation, the difference between 18 hours and 12 hours could be easily due to how well the compared methods were implemented, and how the GPU kernels are parameterized. They give no details, and no code, so we have to assume they chose results that look favorable.

3) They perform or report no serious validation procedure that will give them an estimation of the generalization error, and therefor no evidence to support the suggestion that the trained network can then be used for multiple runs with different initial conditions and observations. At least we do not know what the error will be. In order to know this, they would have had to perform cross validation or some other resampling method to rigorously test the model on conditions that it didn't see in training (note that running the traditional solver with those conditions is required first in order for the model to see those conditions in training). And we are left without a good idea if the training was sufficient enough that the model would generalize, and to what degree it was just memorizing partial results that are only valid for their training data.

Anyways, an honest assessment is that they were able to find a case where an implementation of their method (including training time) was about 1.4 times faster than an unnamed traditional method+implementation. And the authors speculate that their model could generalize, which would allow applications to new simulation runs without complete re-training. And there is no way to tell if any of it is true. But it's still interesting.

 

[wrobel]

"It’s also much more generalizable, capable of solving entire families of PDEs—such as the Navier-Stokes equation for any type of fluid—without needing retraining. Finally, it is 1,000 times faster than traditional mathematical formulas, which would ease our reliance on supercomputers and increase our computational capacity to model even bigger problems"

as for me that is enough to stop reading