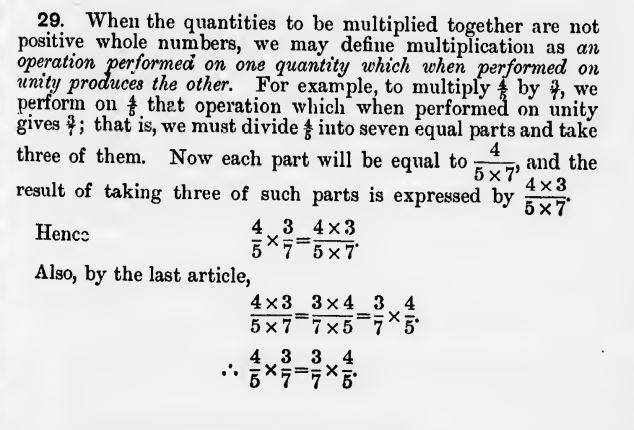Definition of multiplying fractions -- help please

[drooble122]

Homework Statement

"an operation performed on one quantity which when performed on unity produces the other"

Relevant Equations

None

So the part in italics "an operation performed on one quantity which when performed on unity produces the other." I do not understand. Can anyone help me understand what this means? I know how to multiply fractions, but this explanation is confounding to me.

 

[Drakkith]

Let A = 1/2 and B = 3/4.
To get A*B we define multiplication on A by B to be an operation performed on A that, when performed on 1, gives us B.
So to get B we divide 1 by 4 to get 4 equal pieces and then take 3 of them to get 3/4.
To get A*B we divide A into 4 pieces and then take three of them.

The operation we performed on unity was to divide by 4 and then add three of those pieces together. This operation gives us B since we got 3/4 by performing the operation and B = 3/4.
The same operation is then performed on A to yield A*B: 1/2 divided by 4 equals 1/8. Three of those pieces added together gives us 3/8. Or, in short, 1/2*3/4 = 3/8.

If B was 4/5 instead then the operation would be that which when performed on 1 gives us 4/5, which is to divide by 5 and add 4 of those pieces together.

 

[drooble122]

Thank you very much! I understand now!

 

[Mark44]

@drooble122, based on the image you attached, it appears that you are using a very old textbook. I would advise getting something (anything!) a bit more modern.

Most textbooks on arithmetic define the multiplication of fractions like this:
$$\frac a b \times \frac c d = \frac{ac}{bd}$$
and let it go at that, with no extraneous wordage.

The example given, $\frac 4 5 \times \frac 3 7 = \frac{4 \times 3}{5 \times 7} = \frac{12}{35}$. Usually, if there are common factors in the numerator and denominator, these would be removed. In this example, there are no factors common to both 12 and 35, so the answer above would be the final result.