- #1
McFluffy
- 37
- 1
Suppose if we have a cube:
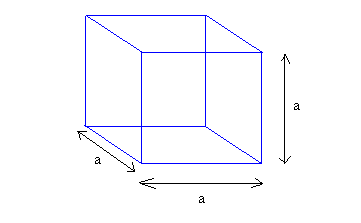
The volume of the cube is the product of the length, width and the height. All this time, I've been looking at it as: To get the volume, multiply the area of the cross section of the cube by how many "layers" it has. To elaborate with the diagram given, one can see that the above image is a cube. But how I see it is that, if you have a square of length ##a## and stack ##a## amount of "layers" above/beside/behind/whatever direction such that it is perpendicular the square, you'll form a cube. My question is that, is this a wrong way to look at volumes in general? If it is, why is it wrong and what is the correct definition? I searched the internet but I can't find any satisfying answer. I see definitions that state that volume is defined as how much space can a closed surface contain but that's just a bit vague for me.
The volume of the cube is the product of the length, width and the height. All this time, I've been looking at it as: To get the volume, multiply the area of the cross section of the cube by how many "layers" it has. To elaborate with the diagram given, one can see that the above image is a cube. But how I see it is that, if you have a square of length ##a## and stack ##a## amount of "layers" above/beside/behind/whatever direction such that it is perpendicular the square, you'll form a cube. My question is that, is this a wrong way to look at volumes in general? If it is, why is it wrong and what is the correct definition? I searched the internet but I can't find any satisfying answer. I see definitions that state that volume is defined as how much space can a closed surface contain but that's just a bit vague for me.