Deflection/diffraction of static electric field

[zrek]

I know the fenomenon of diffraction (one slit) in case of electromagnetic waves.
http://en.wikipedia.org/wiki/Diffraction

What happens if there is only a static electric field?

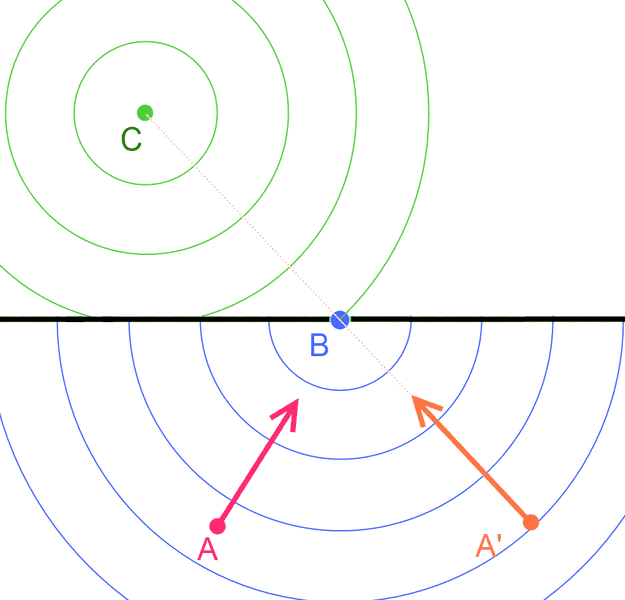
There is a point-like charge at the point C.
The black line is a wall that blocks the electric field.
At the point B there is a hole in the wall.
A and A' are test charges to measure the force, the field direction.

What we will measure?
Possible answers:

1: The picture is correct, at the point A the force directs to the hole, the point B. The test charge A will feel a force which is as big as it would come from the distance AB+BC.
2: This experiment is not possible, there is no way to block the static electric field by a wall.
3: The electric field "flows through" the hole, but the force on the test charge A will still direct to the point C. The measured force will as big as it would come from a distance AB+BC.
4: The electric field "flows through" the hole, but the force on the test charge A will still direct to the point C. The measured force will as big as it would come from a distance AC, just like as it would be without the wall.
5: There is no flowing or deflection or diffraction. The point A will feel no force at all. The test charge at A' have straight view to the C, so will feel the force, as it is on the picture, as big as it would feel without the wall.
6: There is no flowing or deflection or diffraction. The point A will feel no force at all. The test charge at A' have straight view to the C, so will feel the force, but a weaker one than it would be without the wall.
7: Other possibilities?

What do you think, which is the correct answer?

Thank you!

 

[Jano L.]

A wall made of metal would do. The charges will feel some weak force, depending on how great is the hole in the wall. however, this forces need not point to the hole, nor to the charge C. More concrete answers would probably require to calculate the potential via the Poisson equation.

 

[zrek]

Great, thank you for your answer.

A wall made of metal would do. The charges will feel some weak force, depending on how great is the hole in the wall.

If I understand it well then you mean that the force depends only on how the electric field "flows through" the hole, and it is independent from the effect of the wall itself, right? If there would be no hole at all, the test charge would feel no force, right? I mean that I'd like to examine a case where I can assume that the wall itself is perfectly blocks the electric field, and only the hole gives a possibility to make effect on the other side.
Is this the case that you are talking about?
I'm not interested in a case where the block is because of a permittivity of the wall, this would result an effect of the wall too. I'd like to assume a theoretic case, when the wall blocks completely the field and have no effect on the field at the other side at all.
Is this the case when I can use the Poisson equation somehow?

More concrete answers would probably require to calculate the potential via the Poisson equation.

I'd like to make exact calculations. Would you be so kind and help me how to start? Is there a document on the net, which is about the calculation like this? I'd like to see and analyse an example of a calculation.
Thank you for your help!

 

[physwizard]

I'd like to make exact calculations. Would you be so kind and help me how to start? Is there a document on the net, which is about the calculation like this? I'd like to see and analyse an example of a calculation.
Thank you for your help!

I think you could try using some simulation software, or PDE solver software to figure out how the field lines would look like. Or else you could try to write some code for it in mathematica or maple.
If you want to try solving it analytically ( This may be a bit difficult and require some approximations/simplifications. ) Jackson is the best reference - first three chapters. I believe he has solved a similar (but simpler) problem involving a circular hole in a metallic sheet.

 

[zrek]

Well, I tought that my case is a simple case, since it can degrade to 2D and contains only few and not so special limits.

PDE solver software to figure out how the field lines would look like.

Thank you for the adice, I'll try it somehow. I'd be satisfied with this possibility. Can you give me an advice about where can find an good (free, online?) PDE solver software?

Jackson is the best reference - first three chapters. I believe he has solved a similar (but simpler) problem involving a circular hole in a metallic sheet.

This solved problem would be perfect for me. I'll search for it, thank you for the tip.

 

[physwizard]

Well, I tought that my case is a simple case, since it can degrade to 2D and contains only few and not so special limits.

Its a 3D problem as there is no symmetry. But worth giving a try.

Thank you for the adice, I'll try it somehow. I'd be satisfied with this possibility. Can you give me an advice about where can find an good (free, online?) PDE solver software?

Unfortunately, I don't know much about the free packages, haven't tried them out so far.

This solved problem would be perfect for me. I'll search for it, thank you for the tip.

It can give you a picture. But I think your approach would be different from this one because this textbook problem has azimuthal symmetry whereas this problem doesn't.

 

[zrek]

OK, thank you, now I understand that the example is not a simple case. I still would like to solve it, but for the beginning I'd like to solve a simplier case. Do you think that the case below is more simple?

My main objective is to understand the possibility of the deflection of the static electric field, and then solve a concrete case. So first I'd like to analyze a simple case.

Above the blocking wall there is a homogeneous electric field. B is a hole and A is a negative test charge. I'd like to calculate the force on it.
Which is (are) the correct statement(s) in this case?

1. The force points to the hole.
2. The picture is not good, the force points perpendicular to the wall.
3. The smaller hole, the more circle-like are the isolines

Thank you!

 

[physwizard]

View attachment 58869

My main objective is to understand the possibility of the deflection of the static electric field, and then solve a concrete case. So first I'd like to analyze a simple case.

Above the blocking wall there is a homogeneous electric field. B is a hole and A is a negative test charge. I'd like to calculate the force on it.
Which is (are) the correct statement(s) in this case?

1. The force points to the hole.
2. The picture is not good, the force points perpendicular to the wall.
3. The smaller hole, the more circle-like are the isolines

Thank you!

I assume that the sheet in your diagram is conducting and grounded, otherwise it would not prevent the electric field from penetrating to the other side.
I guess you are trying to find out whether the electric field penetrates to the other side if there is a hole, and to what extent.
Yes, you can expect the force to point away from the hole for distances close to the hole and go to zero at larger distances.
As mentioned, Jackson has solved a similar example. To quote him "The distribution (of potential) is rotationally symmetric about the vertical line through the center of the hole. At distances more than two or three times the radius away from the hole, the presence (of the electric field) is hardly discernible."

OK, thank you, now I understand that the example is not a simple case. I still would like to solve it, but for the beginning I'd like to solve a simplier case. Do you think that the case below is more simple?

I'm not sure if this makes things any simpler. These 'infinite sheet of charge' problems are a bit contrived since in practice you would always encounter localized charge distributions whose fields can be assumed to go to zero at infinity.
If your purpose is to try and see if the electric field can penetrate to the other side if there is a hole, maybe you could try out the case of a point charge at the centre of a thin grounded conducting (hollow) sphere with a circular hole.

 

[zrek]

This is very good, I think that I got a confirmation that basicaly I'm thinking well about this.
What I assume is that if the hole size approaches zero, the hole will behave like a point-like charge.

If I understand well, you suggest to work me on this (below) since it will be easier to calculate with:

OK, I'll try to analyze this, thanks again for your help.

 

[physwizard]

Hi, I did try solving this analytically but ran into a few difficulties. Then I tried solving a similar problem in two dimensions but ran into difficulties there as well. I have posted my question in the differential equations forum. But I am still to get an answer to that. This is where I have posted my question: https://www.physicsforums.com/showthread.php?t=692974
If any of you are able to answer this question please do. Thanks.

 

[HomogenousCow]

Hm..Could you just model the sheet as a boundary, and impose a dirac delta function on it, modelling a very small hole.

 

[zrek]

If any of you are able to answer this question please do. Thanks.

Unfortunately I have no good idea on it, I hope that finally it will be solved.
Thank you for letting me know that you are thinking on this problem, you are great.

I'm still thinking and working on this too, but have not yet found a stable solution.

 

[zrek]

Hm..Could you just model the sheet as a boundary, and impose a dirac delta function on it, modelling a very small hole.

Thanks, but I unfortunately failed to handle the dirac delta in a PDE. I think that maybe by using the dirac delta, I'll arrive to a false result. Seems to me that it is better if I try to solve the problem by searching for the possibilities what happens if the hole size approaches the zero.

 

[HomogenousCow]

The diagram is a bit misleading, we're talking about a static field here?

 

[Jano L.]

I think I was wrong about this earlier. In the case of the charge at the centre of the hollow grounded spherical shell with a circular hole, I suspect that the field outside will be exactly zero.

Why ? I do not think so. The field will be continuous across the hole, and inside it is non-zero.

 

[physwizard]

Why ? I do not think so. The field will be continuous across the hole, and inside it is non-zero.

Okay, I just deleted that post because I was not sure about some of the aspects. In the case of the point charge at the centre of the grounded conducting spherical shell with a circular hole, yes the field will be continuous across the hole, it will be non-zero inside, but it will be zero outside whether or not there is a hole. I cannot give a concrete reasoning for this yet, it is just a suspicion.

 

[Jano L.]

The solution depends continuously on the size of the hole. Imagine that the hole is so large that one half of the sphere is missing. Do you think the field will be still zero outside the implied imaginary sphere? I think you will agree with me that it will not. Now shrink the hole. What will happen?

 

[physwizard]

The solution depends continuously on the size of the hole. Imagine that the hole is so large that one half of the sphere is missing. Do you think the field will be still zero outside the implied imaginary sphere? I think you will agree with me that it will not. Now shrink the hole. What will happen?

You're quite right, actually. But how to solve the damn problem? The continuity of the electric field at the hole is stumping me. I guess the solution for a sphere needs to be patched up by a component which makes the electric field continuous at the hole.