Deflection of a Beam: Simple Solutions for Calculations

[rsq_a]

I have the following problem, which involves a two-dimensional curved and thin beam with profile given by y= f(x). You can assume that the beam is only weakly curved (and so slopes are all quite small).

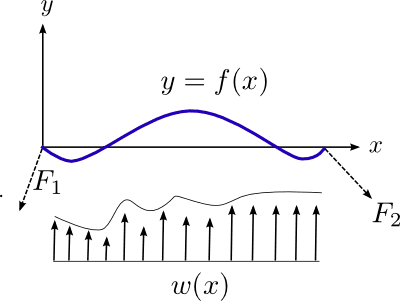
The beam's free-ends are both subjected to a force F1 and F2 (which will be given) and is also subjected to a load, w(x), directed vertically upwards.

Is there a simple question which gives the deflection of the beam?

 

[Studiot]

Can't see why your profile takes on the blue curve as shown, with the loads shown, perhaps you can supply more details?

Is this coursework or what?

 

[rsq_a]

Can't see why your profile takes on the blue curve as shown, with the loads shown, perhaps you can supply more details?

The loads are arbitrary (some arbitrary load, w(x) will be applied). The blue curve is some arbitrary curve which represents the unstressed beam.

Is this coursework or what?

No, it's not coursework.

 

[Studiot]

So the beam is pre-bent?

I suppose you could subtract f(x) from the elastic curve which is a solution to the fourth order differential equation of the beam.
You will need enough known boundary conditions to find the constants of integration.

 

[rsq_a]

So the beam is pre-bent?

I suppose you could subtract f(x) from the elastic curve which is a solution to the fourth order differential equation of the beam.
You will need enough known boundary conditions to find the constants of integration.

Can you explain why you think this would be valid? As I understand it, the derivation of the beam equations for a curved beam would have to differ from the derivation for a straight beam.

 

[Studiot]

You can assume that the beam is only weakly curved (and so slopes are all quite small).

You have already specified that the beam is nearly straight.
You only use curved beam theory for seriously curved beams.