Deflection of L Shaped Cantilever Beam

[Wil_K]

Homework Statement

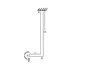
I would like to know how to find the horizontal and vertical deflection of point C shown in the attached diagram. I also need to find the angle of deflection for point C.

Homework Equations

The Attempt at a Solution

I've already found a solution to this problem, but I'm not sure if it's correct. I figured that the vertical deflection can be found by analysing the horizontal member using: δv = ML^2/2EI. Then I replaced the moment with an equivalent point load acting at C, which gives the same deflection. Then I found the moment acting about point B as a result of the equivalent point load, and used the above formula to find the horizontal deflection of the vertical member.

For the total angle of deflection I just added the deflection angles for each section, which were found using: ∅= ML/EI = PL^2/2EI.

I have doubts that this is the correct solution, so it would be great if someone could steer me in the right direction.

 

[haruspex]

Then I replaced the moment with an equivalent point load acting at C

You cannot in general simply replace a torque with a force. It may exert the correct torque about some point, but not about all points, and it will exert a linear force which the torque did not.
A torque is applied to BC. For equilibrium of BC, AB must exert an equal and opposite torque, but no linear force, on BC. Similarly, the support at A must exert a pure torque on AB.

 

[Lnewqban]

That applied torque M is transferred unchanged all the way until reaching the anchoring point A, where a reactive equal and opposite moment appears.
The deflection of each length of the L-shaped part depends on how long each one of those is.

 

[haruspex]

The deflection of each length of the L-shaped part depends on how long each one of those is.

Not sure what you mean by that. The moment will bend AB, causing a displacement of B, and bend BC, causing a displacement of C relative to the displaced B.

 

[Lnewqban]

Not sure what you mean by that. The moment will bend AB, causing a displacement of B, and bend BC, causing a displacement of C relative to the displaced B.

Yes, I was thinking of horizontal displacement of B (and C) and vertical displacement of C.