erobz
Gold Member
- 4,445
- 1,839
- Homework Statement
- Determine the density distribution ##\rho (u)## along the tube as the piston advances
- Relevant Equations
- Conservation of Mass
I'm trying to figure out how describe the mass of air between the piston face and the und of the tube ( position ##o##) in the acompanying diagram.
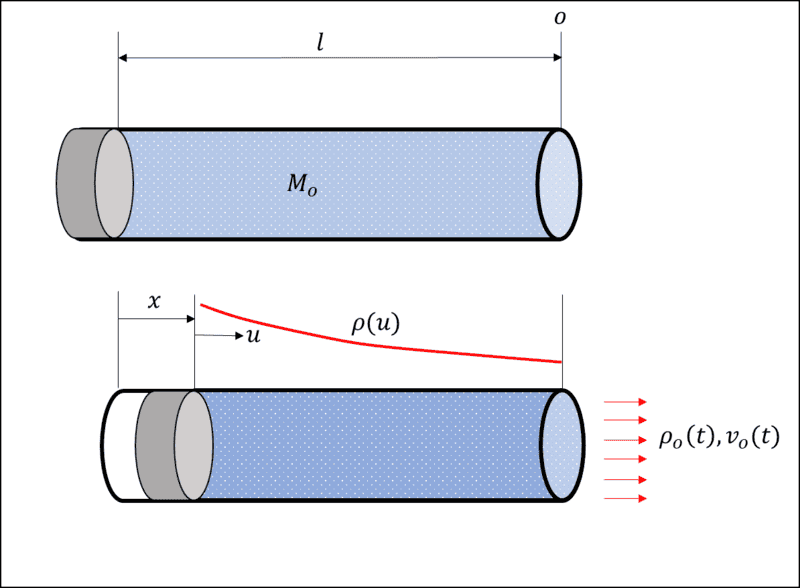
At ##t = 0##, the mass of air in the tube is ##M_o##, and the system is static with tube length ##l##. The ##x## coordinate describes how far along the tube the piston has advanced at time ##t##. The ##u## coordinate ranges from the piston face to the end of the tube ## 0 \leq u \leq l-x ##
Let the density, and velocity (both assumed to be uniformly distributed over the cross section) of the outflow be given by ##\rho_o (t), v_o(t)##respectively.
Applying conservation of mass I get the following relationship:
$$ A \int_0^{ l-x(t) } \rho (u) ~du = M_o - A \int_0^t \rho_o (t) v_o (t) ~dt$$
Where ##A## is the cross sectional area of the tube, and the ##x## coordinate is given by:
$$x(t) = \int_0^t \dot x ~dt $$
My goal is to get ##\rho (u)## as a function of all the other variables. My instinct is to try transform ##du \to k ~dt ## and then differentiate both sides w.r.t. ##t##.
? Is it ok to write:
$$ \begin{aligned} u &= l-x \\ & = l - \int_0^t \dot x ~dt \\ \implies & \frac{du}{dt} = -\dot x \end{aligned} $$
Substituting for ##du## :
$$ -A \int_0^{ l-x(t) } \rho (u) ~\dot x ~dt = M_o - A \int_0^t \rho_o (t) v_o (t) ~dt$$
Now differentiate both sides w.r.t time ##t##:
$$ -A \frac{d}{dt} \left( \int_0^{ l-x(t) } \rho (u) ~\dot x ~dt \right) = \cancel {\frac{d}{dt} M_o}^0 - A \frac{d}{dt} \left( \int_0^t \rho_o (t) v_o (t) ~dt \right) $$
$$ \boxed{ \implies \rho(u) \dot x = \rho_o(t) v_o(t) } $$
Possibly I've performed some unsavory mathematics?
At ##t = 0##, the mass of air in the tube is ##M_o##, and the system is static with tube length ##l##. The ##x## coordinate describes how far along the tube the piston has advanced at time ##t##. The ##u## coordinate ranges from the piston face to the end of the tube ## 0 \leq u \leq l-x ##
Let the density, and velocity (both assumed to be uniformly distributed over the cross section) of the outflow be given by ##\rho_o (t), v_o(t)##respectively.
Applying conservation of mass I get the following relationship:
$$ A \int_0^{ l-x(t) } \rho (u) ~du = M_o - A \int_0^t \rho_o (t) v_o (t) ~dt$$
Where ##A## is the cross sectional area of the tube, and the ##x## coordinate is given by:
$$x(t) = \int_0^t \dot x ~dt $$
My goal is to get ##\rho (u)## as a function of all the other variables. My instinct is to try transform ##du \to k ~dt ## and then differentiate both sides w.r.t. ##t##.
? Is it ok to write:
$$ \begin{aligned} u &= l-x \\ & = l - \int_0^t \dot x ~dt \\ \implies & \frac{du}{dt} = -\dot x \end{aligned} $$
Substituting for ##du## :
$$ -A \int_0^{ l-x(t) } \rho (u) ~\dot x ~dt = M_o - A \int_0^t \rho_o (t) v_o (t) ~dt$$
Now differentiate both sides w.r.t time ##t##:
$$ -A \frac{d}{dt} \left( \int_0^{ l-x(t) } \rho (u) ~\dot x ~dt \right) = \cancel {\frac{d}{dt} M_o}^0 - A \frac{d}{dt} \left( \int_0^t \rho_o (t) v_o (t) ~dt \right) $$
$$ \boxed{ \implies \rho(u) \dot x = \rho_o(t) v_o(t) } $$
Possibly I've performed some unsavory mathematics?
Last edited: