- #1
genxium
- 141
- 2
As learning laser fundumentals, I've just reviewed the boundary conditions for electromagnetic waves.
However, I came back to a point that confused me in the past and want to get it clear now :)
One of the boundary conditions, regarding the magnetic fields parallel to the medium-interface is
[itex]H_{1//}-H_{2//}=J_s[/itex]
where [itex]H_{1//} \; and \; H_{2//} \; \text{are magnetic field strengths and} \; J_s \; \text{is the electric current per unit area} [/itex].
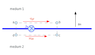
I found the derivation in my textbook elements of engineering electromagnetics (6th edition) by Nannapaneni Narayana Rao: (please view the attachment to find corresponding notations):
[itex]\oint_{C} \vec{H} \cdot d\vec{l} = \int_{S} \vec{J} \cdot d\vec{s} + \frac{d \int_{S} \vec{D} \cdot d\vec{s}}{d \, t}[/itex]
Note that [itex]bc \approx 0 \; and \; da \approx 0[/itex] so that flux of electric fields is ignored, hence
[itex]ab \cdot H_{1//}+bc \cdot H_{\perp}+ cd \cdot H_{2//}+ da \cdot H_{\perp}= J_s \cdot AREA_{abcd}[/itex]
where [itex]ab=-cd, \; bc=-da[/itex], thus
[itex]ab \cdot H_{1//}- ab \cdot H_{2//} = J_s \cdot AREA_{abcd}[/itex]
and now, I just can't get [itex]H_{1//}-H_{2//}=J_s[/itex] because [itex]\frac{AREA_{abcd}}{ab} \not= 1[/itex].
Would anyone help to point out where I'm wrong or share some good references?
However, I came back to a point that confused me in the past and want to get it clear now :)
One of the boundary conditions, regarding the magnetic fields parallel to the medium-interface is
[itex]H_{1//}-H_{2//}=J_s[/itex]
where [itex]H_{1//} \; and \; H_{2//} \; \text{are magnetic field strengths and} \; J_s \; \text{is the electric current per unit area} [/itex].
I found the derivation in my textbook elements of engineering electromagnetics (6th edition) by Nannapaneni Narayana Rao: (please view the attachment to find corresponding notations):
[itex]\oint_{C} \vec{H} \cdot d\vec{l} = \int_{S} \vec{J} \cdot d\vec{s} + \frac{d \int_{S} \vec{D} \cdot d\vec{s}}{d \, t}[/itex]
Note that [itex]bc \approx 0 \; and \; da \approx 0[/itex] so that flux of electric fields is ignored, hence
[itex]ab \cdot H_{1//}+bc \cdot H_{\perp}+ cd \cdot H_{2//}+ da \cdot H_{\perp}= J_s \cdot AREA_{abcd}[/itex]
where [itex]ab=-cd, \; bc=-da[/itex], thus
[itex]ab \cdot H_{1//}- ab \cdot H_{2//} = J_s \cdot AREA_{abcd}[/itex]
and now, I just can't get [itex]H_{1//}-H_{2//}=J_s[/itex] because [itex]\frac{AREA_{abcd}}{ab} \not= 1[/itex].
Would anyone help to point out where I'm wrong or share some good references?