Mart1234
- 6
- 0
- TL;DR Summary
- Question dealing with the derivation of the generalized Khon-Sham equations regarding the final eigenvalue.
Hello, I am following the paper: https://www.yumpu.com/en/document/read/42212557/exact-exchange-in-density-functional-calculations and I am confused on page 14 where the generalized Kohn-Sham equations are derived. I follow that the ground state energy is
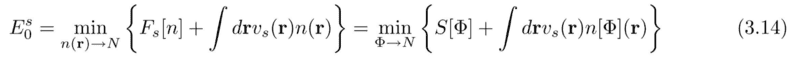
The minimization of this step leads to
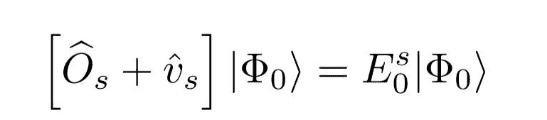 .
.
where
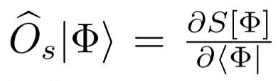
I'm not sure of the process used to generate this eigenvalue problem. Any insight into how this was done or other resources would be greatly appreciated.
The minimization of this step leads to
where
I'm not sure of the process used to generate this eigenvalue problem. Any insight into how this was done or other resources would be greatly appreciated.