Derivation of Griffith's Criterion

[person123]

TL;DR Summary

I am attempting to derive Griffith's Criterion to understand it better. My derivation matches up to a constant which I don't fully understand.

I did my derivation for a beam as shown with Young's Modulus $E$, width $w$, crack length $a$, and surface energy density $\gamma$.

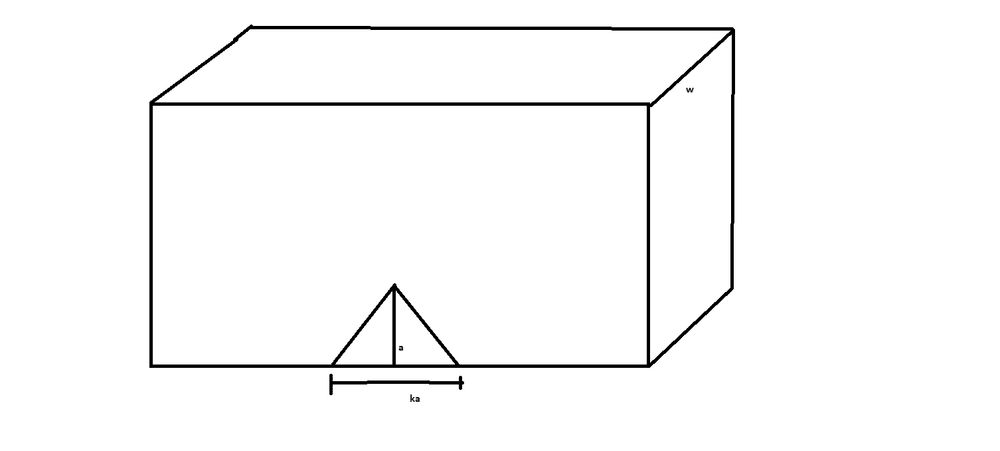
I understand that a crack will propagate when the free energy $G$ decreases with increase crack length $a$. Free energy is the combination of the elastic energy $U$ and surface energy $S$ with the equation $$G=S-U.$$ This means that $$\frac{dS}{da}=\frac{dU}{da}$$ at the moment $G$ starts decreasing. I believe $$S=\gamma w a$$ meaning $$\frac{dS}{da}=\gamma w.$$ I then assumed that the potential energy would be released due to the crack over the triangular region shown in the diagram. $k$ is a constant which I don't know. Based on this, analyzing the elastic energy along one horizontal slice $$dU=\frac{\sigma_f^2}{E}wdA=\frac{\sigma_f^2}{E}wkada$$ $$\frac{dU}{da}=wka\frac{\sigma_f^2}{E}.$$ Equating the two: $$\gamma w=wka\frac{\sigma_f^2}{E}$$ $$\sigma_f^2=\frac{E\gamma}{ka}.$$ If $k$ is defined as $\frac{\pi}{2}$ then my equation matches with Griffith's criterion. However, I don't understand where $\pi$ comes from. Is my approach correct, and if so how would one go about completing this derivation? Thanks!

 

[Achy47]

Hello,

Your approach seems to be generally correct. The $k$ value in this case is known as the stress intensity factor and it is used to account for the stress concentration at the tip of the crack. The value of $\pi$ comes from the geometry of the triangular region that you have assumed for the potential energy release. This geometry is often used in fracture mechanics analyses and it is based on the assumption that the crack will grow along the path of maximum stress intensity. This path is at an angle of $\frac{\pi}{2}$ to the original crack length, hence the value of $\pi$ in the stress intensity factor.

If you want to complete the derivation, you can use the value of $\sigma_f$ that you have calculated and substitute it into the equation for free energy $G$. Then, you can differentiate $G$ with respect to $a$ and set it equal to 0 to find the critical crack length at which the free energy starts to decrease. This will give you the critical crack length according to Griffith's criterion.

I hope this helps. Let me know if you have any further questions.