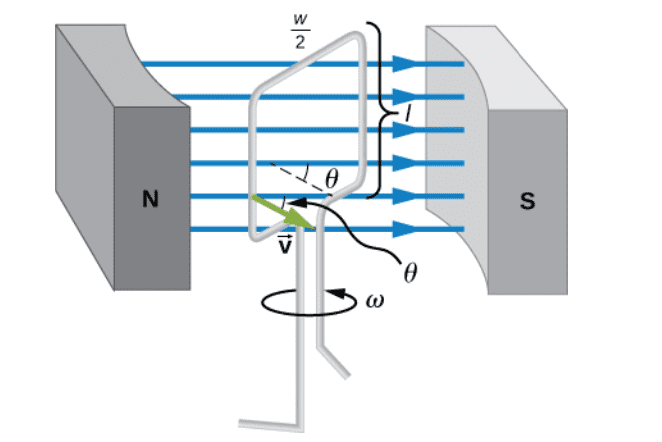
alan123hk said:
I feel like I's starting to understand the meaning of ##\vec{j}=\sigma \left (\vec{E} + \frac{1}{\rho} \vec{j} \times \vec{B} \right)##. Although I don't know how to apply it in a practical situation, because the math seems to get very complicated, e.g. the motion trajectory of electric charge is not restricted to very thin wires, but can move freely in 3D space. But anyway, it's a really cool expression.
On the other hand, I agree that the Lorentz Force ##~\vec{F_L}=(\vec{B}\times \vec{v})q_e## should not be interpreted as an electric field force ##\vec{F_E}=\vec{E}q_e ## because it was zero unless the charge are moving. But the electric field created by magnetic EMF ##(2Blv~sin~\theta )~##is of course real, because this electric field is created by the charge that accumulates on the conductor after being moved by the force ##~\vec{F_L}=(\vec{B}\times \vec{v})q_e##.
The most simple way to understand this constitutive equation is Drude's model of a conductor: A metall consists of a lattice consisting of positively charged ions, and we'll work in the rest frame of this ion lattice. Within this ion lattice the conduction electrons can flow nearly freely (in other words they are not bound to individual atoms but delocalized over the entire metal).
Now set these conduction electrons into motion, e.g., by applying some external electromagnetic field. The equation of motion of such an electron (for simplicity I use the non-relativistic approximation here) then reads
$$m \ddot{\vec{x}}=-m \gamma \dot{\vec{x}}-e (\vec{E}+\vec{\dot{x}} \times \vec{B}),$$
where ##\vec{E}## and ##\vec{B}## are the total fields at the place of the electron, i.e., the external field + the field due to the charge-current distribution within the metal. The first force term on the right-hand side takes into account the scatterings of the electrons with defects of the ion lattice (including their thermal motion) in terms of a linear friction term.
If you make the external fields either time-independent or varying only slowly with time (i.e., the time scale of the variations of the fields is much larger than the typical "relaxation time", ##\tau=1/\gamma##). Then you can assume that the electrons are always accelerated so far that the friction force compensates the electromagnetic force. Then you have
$$\dot{\vec{x}}=-\frac{e}{m\gamma} (\vec{E}+\vec{\dot{x}} \times \vec{B}).$$
To get the current density you have to multiply this with ##\rho=-e n##, where ##\rho## is the charge density of the conduction electrons and ##n## their number density. From this you get Ohm's Law,
$$\vec{j}=\frac{n e^2}{m \gamma} (\vec{E} + \vec{v} \times \vec{B})=\sigma (\vec{E}+\frac{\vec{j}}{\rho} \times \vec{B}).$$
For usual "house-hold currents" an estimate gives that the velocity is about 1mm/s, and thus usually the part involving the magnetic field can safely be neglected.
An exception is when it comes to the examples like the one considered here, where the metal (i.e., the ion lattice) is moving in external magnetic fields. Then you have to take the term with the magnetic field into account, and it is a safe approximation to use the external magnetic field for ##\vec{B}## and the velocity ##\vec{u}## of the wire for ##\dot{\vec{x}}##. The velocity the conduction electrons against the wire is again very small and can be neglected (as well as the magnetic field unduced by this current).
Other exceptions are the correct treatment of the homopolar generator as well as the fully relativistic treatment of the current-conducting wire. For both I've written Insights. The pdf versions are
https://itp.uni-frankfurt.de/~hees/pf-faq/homopolar.pdf
https://itp.uni-frankfurt.de/~hees/pf-faq/relativistic-dc.pdf