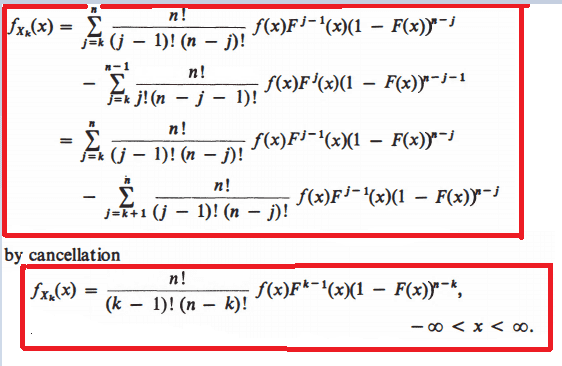I tag this question as "SOLVED". I understood all the computations. Thanks.WMDhamnekar said:Summary: If ## F_{X_k}(x) = p(X \leq x) = \displaystyle\sum_{j=k}^n \binom{n}{j} F^j(x)(1-F(x))^{n-j}, -\infty
< x < \infty ## then how to prove ##f_{X_k} (x) =\frac{n!}{(k-1)!(n-k)!}f(x) F^{k-1}(x)(1-F(x))^{n-k}##
Author computed ##f_{X_k}(x)## as follows but I don't understand it. Would any member explain me the following computations?
A P.D.F. (Probability Density Function) is a mathematical function that describes the probability of a continuous random variable taking on a certain value. A distribution function, also known as a cumulative distribution function, shows the probability that a random variable is less than or equal to a given value.
To derive a P.D.F. from a distribution function, we take the derivative of the distribution function. This results in the probability density function, which can then be used to calculate the probability of a random variable falling within a certain range of values.
Deriving a P.D.F. from a distribution function allows us to understand the probability distribution of a continuous random variable. This information is crucial in many fields, such as statistics, economics, and engineering, as it helps us make predictions and make informed decisions based on data.
One limitation is that the P.D.F. and distribution function only apply to continuous random variables. They cannot be used for discrete random variables. Additionally, the P.D.F. may not exist for all types of distributions, such as those with infinite variance.
No, a P.D.F. only gives the probability of a random variable falling within a range of values. To calculate the probability of a specific value, we need to use the distribution function or integrate the P.D.F. over that specific value.