- #1
Edd257
- 5
- 0
Hi,
The integrals in the image are well-known, but we are not allowed to use them in the test.
I have tried to prove them using changing variable t, but I didn't succeed.
Can you show me the way?
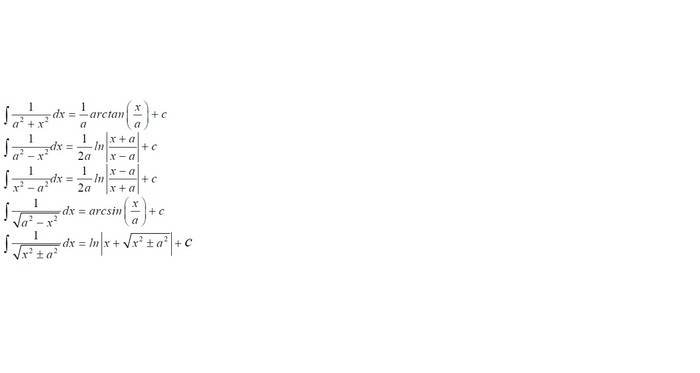
The integrals in the image are well-known, but we are not allowed to use them in the test.
I have tried to prove them using changing variable t, but I didn't succeed.
Can you show me the way?
