Derivative, i.e. D[ ] , of Re [ something ]

[Swamp Thing]

TL;DR Summary

Wolfram tries to apply the chain rule and gets stuck simplifying Re'[something]

Consider these two examples:
D[ Re[ Exp[ I*t ] ], t ]

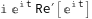
D[Re[Exp[I*t]],t] /. t-> 0.5

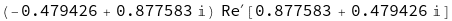
Mathematica seems to get stuck differentiating the "Re[ ]" function after (rather naively) applying the chain rule. This is a trivial example, but we might have a more complicated function defined like :-
myFn [ t _ ]:= Re [(* stuff *)]
... and we would like to find D [ myFn [ t ] ], t] without extra manual reformulation.

How can we do that elegantly and automatically?

 

[Mark44]

Can either Wolfram or Mathematica do the calculation in two steps? I.e., by first calculating $Re(e^{it})$ and then differentiating that result?
Either of these should be able to simplify $Re(e^{it})$, which is just $\cos(t)$.

 

[member 428835]

Can either Wolfram or Mathematica do the calculation in two steps? I.e., by first calculating $Re(e^{it})$ and then differentiating that result?
Either of these should be able to simplify $Re(e^{it})$, which is just $\cos(t)$.

I'd do it like this, which worked for me, giving the desired output $-\sin(t)$:

f[t_] = Exp[I t];
D[ComplexExpand[Re[f[t]]], t]