- #1
- 962
- 667
- TL;DR Summary
- Plotted what should be an analytic function, as a function of real and imaginary part. The slopes are different. Why?
Below are plots of the function ##e^{0.25(x-3)^{-2}} - 0.87 e^{(x-3.5)^{-2}}##
The first plot is for real values. It has a minimum at the red dot. The second plot has in its argument the same real part as the red dot, but has the imaginary part changing from -0.3 to 0.3. It shows the resulting change in the imaginary part of f(z).
For an analytic function (which I believe this one is) the derivatives around any point should be the same, approaching a point from the real and complex directions, but here obviously they are not. What have I got wrong?
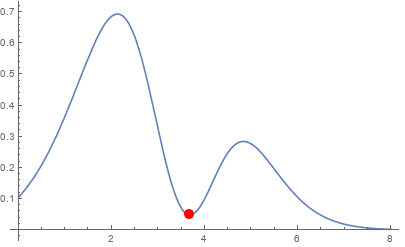
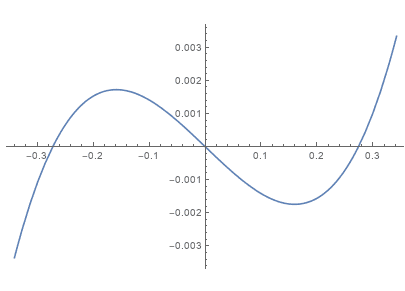
The first plot is for real values. It has a minimum at the red dot. The second plot has in its argument the same real part as the red dot, but has the imaginary part changing from -0.3 to 0.3. It shows the resulting change in the imaginary part of f(z).
For an analytic function (which I believe this one is) the derivatives around any point should be the same, approaching a point from the real and complex directions, but here obviously they are not. What have I got wrong?
Attachments
Last edited: