- #1
mfaisal
- 1
- 0
View attachment 5681
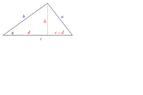
In the above given triangle when θ = 0 then b=c
But when θ = 90 then d=0
Since d is the projection of b
How we can derive a generalised formula for d or c-d with respect to θ
Plese may kindly be elaborated
In the above given triangle when θ = 0 then b=c
But when θ = 90 then d=0
Since d is the projection of b
How we can derive a generalised formula for d or c-d with respect to θ
Plese may kindly be elaborated