- #1
Drain Brain
- 144
- 0
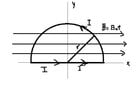
I'm trying to derive a formula for the magnetic torque on a semicircular loop.
what I've done so far is this
The magnetic force on the non-curved loop is
$\vec{F}_{x}=\int Idx\hat{i}\times B_{\circ}\hat{i}=0N$
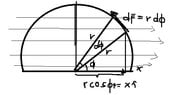
for the curved loop
$\vec{F}_{c}=\int_{0}^{\pi} Ird\phi\hat{\phi}\times B_{\circ}\hat{r}=-2B_{\circ}Ir\hat{k}$I'm not sure if what I've done is correct. This is all I can do. Can you please help me finish it. Thanks!
Attachments
Last edited: