- #1
trojsi
- 19
- 0
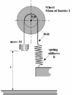
I am asked to derive a formula from the diagram attached. I should end up with this equation:
[tex]f=1/2\pi (k/(M+I/R^2))[/tex]
I tried really hard relating linear quantities with rotational (T=Fr, T=I*alpha etc.) ones but it was all in vain.
Any help would be really appreciated.
thanks
[tex]f=1/2\pi (k/(M+I/R^2))[/tex]
I tried really hard relating linear quantities with rotational (T=Fr, T=I*alpha etc.) ones but it was all in vain.
Any help would be really appreciated.
thanks