Deriving the 1-D Linear Convection Equation

[Mr_Acceleration]

With the assumptions of Inviscid flow, no pressure gradient and no body force terms in 1-D Navier Stokes becomes 1-D nonlinear convection equation;

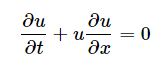
And if we assume velocity of wave propagation is constant value c, equation becomes 1-D linear convection equation;

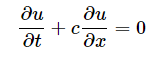
This is online derivation and my question is why only the u value outside of partial derivatives is replaced with c? we have 3 u term there. I was thinking they were all same term. So why do we only replace one of them?

 

[dRic2]

I don't think this is correct. Can you please provide the full derivation ?

 

[Mr_Acceleration]

I don't think this is correct. Can you please provide the full derivation ?

Here is the derivation.

 

[dRic2]

This is correct so far. The problem is this:

And if we assume velocity of wave propagation is constant value c, equation becomes 1-D linear convection equation;

This is not. That's why I'd like a full derivation.

Anyway the reasoning is the following:
$$ \frac {\partial u} {\partial t} + u \frac {\partial u} {\partial x} = 0$$
is NON-linear. What you usually do is linearize it, by writing $u = u_0 + u'$ where $u_0$ is an unperturbed constant velocity and $u'$ is a small perturbation. If you substitute into the diff equation $\frac {\partial u_0} {\partial t} = \frac {\partial u_0} {\partial x} = 0$ because $u_0$ is a constant. You finally end up with
$$ \frac {\partial u'} {\partial t} + u_0 \frac {\partial u'} {\partial x} = 0$$

 

[Mr_Acceleration]

Thank you for your answer. I didn't know about this. Now i will search linearization with pertubation.