- #1
maistral
- 240
- 17
Hi, it's been a while since I last posted. Anyway, so I went through the trouble of enrolling in two finite element analyses classes and yet, they still don't teach how the 2D formulation has been made. I'll list the things that 'I know' already to get some things clear.
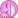 . They were talking about integrations along volumes and there was even an integral with a small circle in the middle! Apparently some deep knowledge in mathematics courses are needed in order to understand these, and most of them involve integrating an entire vector which just made me more dizzy and confused.
. They were talking about integrations along volumes and there was even an integral with a small circle in the middle! Apparently some deep knowledge in mathematics courses are needed in order to understand these, and most of them involve integrating an entire vector which just made me more dizzy and confused.
I actually wanted to avoid those things as I don't know how they would be relevant to me as I'm not really a mathematics major/graduate, I'm an engineering graduate. I am truly sorry for asking help here if it's too much to ask as I really wanted to know where did these things come from, or at least guide me until I achieve the 'unsimplified' but 'clear' solution I wanted - what I'm hoping for is someone be able to guide me with the pertinent theorems in order to arrive with the default, unsimplified formulation similar to the 1D case; something like:
Ti × (insert lengthy integral) + Tj × (insert lengthy integral) + Tk × (insert lengthy integral) = 0.
Anyway, I started off by using the Laplace equation. This is what I have now:
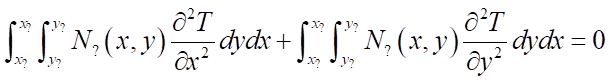
Anyway, these are the questions.
- I know how to derive the 1D finite element formulation using the Galerkin linear weighting functions (in the end I studied this myself as the classes I took did not teach this).
- I know that you can mechanically solve the 1D formulation using the generic force = stiffness matrix × displacement method (this is what I initially knew before taking the undergrad and graduate classes, and yet this is the one they teach here. Yep, waste of money).
- I also know the shape functions for 2D (the triangle thing, where T(x,y) = Ti(xi,yi)Ni(x,y) + Tj(xj,yj)Nj(x,y) + Tk(xk,yk)Nk(x,y) then the weighting functions are Ni(x,y), Nj(x,y), and Nk(x,y), which is integrated to the differential equations as in 1D).
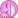 . They were talking about integrations along volumes and there was even an integral with a small circle in the middle! Apparently some deep knowledge in mathematics courses are needed in order to understand these, and most of them involve integrating an entire vector which just made me more dizzy and confused.
. They were talking about integrations along volumes and there was even an integral with a small circle in the middle! Apparently some deep knowledge in mathematics courses are needed in order to understand these, and most of them involve integrating an entire vector which just made me more dizzy and confused.I actually wanted to avoid those things as I don't know how they would be relevant to me as I'm not really a mathematics major/graduate, I'm an engineering graduate. I am truly sorry for asking help here if it's too much to ask as I really wanted to know where did these things come from, or at least guide me until I achieve the 'unsimplified' but 'clear' solution I wanted - what I'm hoping for is someone be able to guide me with the pertinent theorems in order to arrive with the default, unsimplified formulation similar to the 1D case; something like:
Ti × (insert lengthy integral) + Tj × (insert lengthy integral) + Tk × (insert lengthy integral) = 0.
Anyway, I started off by using the Laplace equation. This is what I have now:
Anyway, these are the questions.
- I know I am supposed to multiply the entire PDE with the weighting function. Which weighting function do I use? I remember in the 1D case you have to integrate the differential equations twice, one for the ith case and one for the jth case. Am I correct to assume that I integrate this differential equation thrice, seeing there are three vertices in the triangular element? So that would mean I integrate the PDE; one for the ith, one for the jth case, and one for the kth case?
- I am assuming that you have to use double integration along the x-axis and the y-axis. My problem is about the limits. Which limits do I use? If the bottom limit of the integrands are xi and yi, what would be the upper limit?