JamesBwoii
- 71
- 0
View attachment 3640
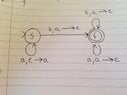
That's the question. I've had a go at drawing a diagram to help me explain it.
View attachment 3641
My understand is that from the start state, an A pushes an A to the stack and stays in the initial state s. Getting a B whilst in state s pops an A from the stack and moves to final state f. Getting a B whilst in state s also pops an A from the stack and remains in state f. And getting an A in the final state whilst A is on the stack remains pops an A from the stack.
How do I describe this language?
I initially thought it might be:
${a^n b^n ∈ {a, b}∗| n ≥ 0}$
but I'm pretty sure that's wrong now.
That's the question. I've had a go at drawing a diagram to help me explain it.
View attachment 3641
My understand is that from the start state, an A pushes an A to the stack and stays in the initial state s. Getting a B whilst in state s pops an A from the stack and moves to final state f. Getting a B whilst in state s also pops an A from the stack and remains in state f. And getting an A in the final state whilst A is on the stack remains pops an A from the stack.
How do I describe this language?
I initially thought it might be:
${a^n b^n ∈ {a, b}∗| n ≥ 0}$
but I'm pretty sure that's wrong now.