mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
- I want to describe in words the following sets:
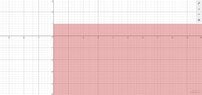
1. $A:=\{(x,y)\in \mathbb{R}^2\mid x>0, y\leq 1\}$
$A$ is the set of all pointgs where the first coordinate is positiv and the second one is less or equal to $1$.
It is the subarea of the plane that is under the point $(0/1)$ to the right, without the y-axis.
Is this description enough or can we say also something else? (Wondering) The graphical representation is:
View attachment 8510
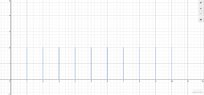
2. $C:=\mathbb{N}\times \{x\in \mathbb{R}\mid 0\leq x\leq 2\}$
$C$ is the cartesian product of the natural number and the interval $[0,2]$. It s the set of points with two coordinates $(n,x)$, where the first coordinate is a natural number and the second coordinate is a real number in the interval $[0,2]$.
What else can we say here? How does the graphical representation look like?
(Wondering)
$$ $$
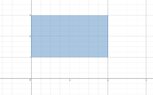
- I want to give also the corresponding set fo the following:
View attachment 8511
It is $\{(x,y)\mid 0\leq x \leq 2, 1\leq y\leq 3\}$, right? Is this enough, or could we also justify that it is like that? (Wondering)
$$ $$
- $F$ is the set of all points in the plane that are at least as far from the origin as $ P = (3 \mid 0) $. Does this mean that we have the set $$F=\{(x,y)\mid x^2+y^2\leq (x-3)^2+y^2\}$$ or have I understood wrong the definition of $F$ ? (Wondering)