Juanda
Gold Member
- 439
- 144
- TL;DR Summary
- I plan to design and print an RC car as a learning experience.
I am planning to design an RC car to 3D print it and have some fun. It will mostly be a learning experience with the by-product of having a hopefully fun RC car by the end of it. That will probably force some decisions that might be overengineered and negatively impact performance but building the very best 3D-printed RC car in the world is out of the scope anyway. Again, learning and having fun is the focus here.
So, to make it more approachable, I would like to design a few iterations growing in complexity. The main parameters for the first iteration would be:
So the steering is where I drew the line in terms of complexity. I could make it without steering but then the car is no fun at all. Could it even be considered a car at that point?
Steering can be quite a complex topic so I would like to keep it as simple as possible. As I read about it, many terms such as slip angle, camber, toe, and bump steer among others came up. For this first and simple iteration, I like to just focus on Ackerman steering and other similar alternatives such as Bell-crank steering.
The following is the typical picture of Ackerman steering geometry. As shown in it, the center of the turning circle is crystal clear in the picture.
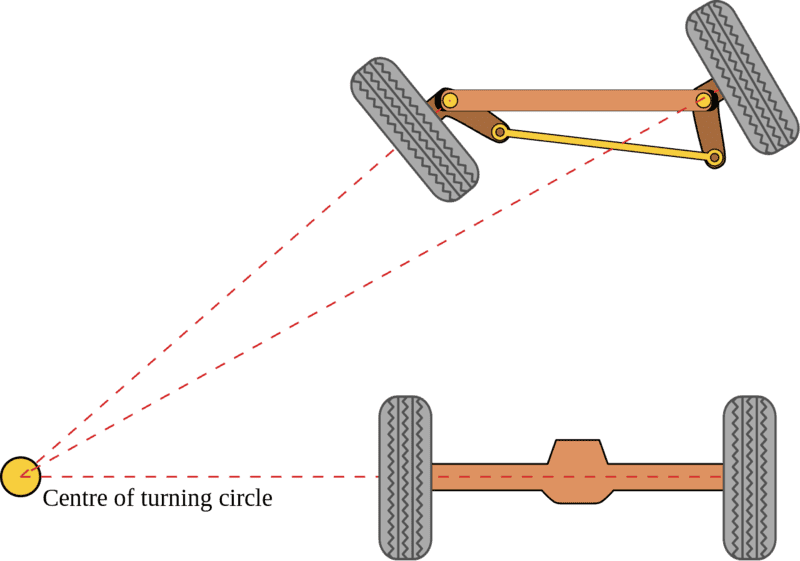
My problem with such a solution is that the shown situation only happens at a particular steering angle. Is that right? I tried some drawings and it's what I seem to obtain from them. For all other angles, the intersection of those three lines will not be at the same point.
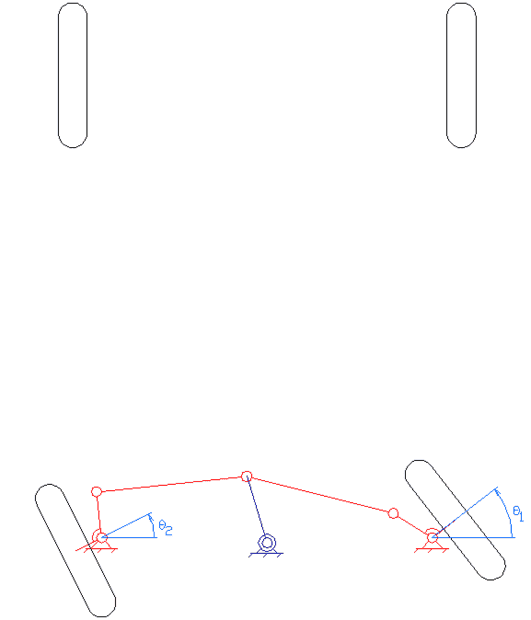
In the case of an Ackerman geometry, the mechanism is just a 4-bar linkage. I wrote some equations to find out if it's possible to design it with such a size ratio so that the intersection happens as in the picture independently of the steering angle but solving the equations is turning out more difficult than initially expected.
Can you confirm if it's possible to design it in such a way as to guarantee the three lines always intersect at one point?
If it's not possible, what's the best approach? To design it so that at full steering angle that condition is fulfilled? Or maybe at half the steering angle because it will occur more frequently?
By the way, I will most likely use a Bell-crank steering because it seems more compatible with a servo but I initially focused the point on the Ackerman mechanism because it's simpler so I'd like to try to understand that one first.
So, to make it more approachable, I would like to design a few iterations growing in complexity. The main parameters for the first iteration would be:
- As many 3D printed parts as possible.
- Only elements commonly found in hardware stores (DIN and ISO standards) can be added except for some key elements such as bearings among others.
- 3D printed gears. They will need to be bulkier but I want to learn to design and print them.
- M3 will be the usual thread size for all joints. Bigger sizes might be considered.
- Rear-wheel drive.
- Solid rear axle.
- No suspension.
- Front-wheel steering.
So the steering is where I drew the line in terms of complexity. I could make it without steering but then the car is no fun at all. Could it even be considered a car at that point?
Steering can be quite a complex topic so I would like to keep it as simple as possible. As I read about it, many terms such as slip angle, camber, toe, and bump steer among others came up. For this first and simple iteration, I like to just focus on Ackerman steering and other similar alternatives such as Bell-crank steering.
The following is the typical picture of Ackerman steering geometry. As shown in it, the center of the turning circle is crystal clear in the picture.
My problem with such a solution is that the shown situation only happens at a particular steering angle. Is that right? I tried some drawings and it's what I seem to obtain from them. For all other angles, the intersection of those three lines will not be at the same point.
In the case of an Ackerman geometry, the mechanism is just a 4-bar linkage. I wrote some equations to find out if it's possible to design it with such a size ratio so that the intersection happens as in the picture independently of the steering angle but solving the equations is turning out more difficult than initially expected.
Can you confirm if it's possible to design it in such a way as to guarantee the three lines always intersect at one point?
If it's not possible, what's the best approach? To design it so that at full steering angle that condition is fulfilled? Or maybe at half the steering angle because it will occur more frequently?
By the way, I will most likely use a Bell-crank steering because it seems more compatible with a servo but I initially focused the point on the Ackerman mechanism because it's simpler so I'd like to try to understand that one first.