Destination Points in Harmonic Sequences

[wheepep]

View attachment 6244

The pattern above will continue for all values of the harmonic sequence.

Will a destination point be reached for any value of θ where 0 ≤ θ < 2𝜋?

(I know it won’t for θ = 0)

Is there a function which contains the set of all destination points?

 

[Opalg]

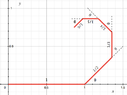
The pattern above will continue for all values of the harmonic sequence.

Will a destination point be reached for any value of θ where 0 ≤ θ < 2𝜋?

(I know it won’t for θ = 0)

Is there a function which contains the set of all destination points?

The answer is Yes. If $0<\theta<2\pi$ then the path will converge to a limit point, which you can find by using complex numbers.

The limit point will be the sum of the series $1 + \tfrac12e^{i\theta} + \tfrac13e^{2i\theta} + \tfrac14e^{3i\theta} + \ldots$. You can sum that series using the power series expansion $\log(1-x) = -x - \frac12x^2 - \frac13x^3 - \ldots$, like this: $$\begin{aligned}1 + \tfrac12e^{i\theta} + \tfrac13e^{2i\theta} + \tfrac14e^{3i\theta} + \ldots &= e^{-i\theta}\sum_1^\infty\frac{e^{in\theta}}n \\ &= -e^{-i\theta}\log\bigl(1 - e^{i\theta}\bigr) \\ &= -e^{-i\theta}\log(1 - \cos\theta - i\sin\theta) \\ &= -e^{-i\theta}\log\bigl( 2\sin^2\tfrac\theta2 - 2i\sin\tfrac\theta2\cos\tfrac\theta2 \bigr) \\ &= -e^{-i\theta}\log\Bigl(2\sin\tfrac\theta2 \cdot e^{i(\theta - \pi)/2}\Bigr) \\ &= (-\cos\theta + i\sin\theta) \bigl(\log \bigl( 2\sin\tfrac\theta2\bigr) + i\tfrac12(\theta - \pi)\bigr) \end{aligned}$$ In terms of coordinates, this shows that your "destination point" is the point $$\Bigl(-\cos\theta\log \bigl( 2\sin\tfrac\theta2\bigr) + \tfrac12(\pi - \theta)\sin\theta\,,\, \sin\theta\log \bigl( 2\sin\tfrac\theta2\bigr) + \tfrac12(\pi - \theta)\cos\theta \Bigr).$$ That looks complicated. But I think it is probably correct because it gives the right result $(\log2,0)$ when $\theta = \pi$. (In that case, the series just becomes $1-\frac12 + \frac13 - \ldots$, which converges to $\log2$ on the real axis.)

If you are asking for a function that has this set of points as its graph, I think you can see that this would be a pretty hard problem. (Worried)

 

[wheepep]

That's great. Thanks!

 

[I like Serena]

Hey wheepep! ;)

Here's the graph of the limit points based on Opalg's formula:

\begin{tikzpicture}
%preamble \usepackage{pgfplots}
\begin{axis}[xmin=0, grid=both, axis lines=middle, axis equal, xlabel=$x$, ylabel=$y$]
\addplot[ultra thick, red, domain=0:3.142, variable=t, samples=51]
( {-cos(deg(t))*ln(2*sin(deg(t/2)))+1/2*(pi-t)*sin(deg(t))},
{sin(deg(t))*ln(2*sin(deg(t/2)))+1/2*(pi-t)*cos(deg(t))} );
\addplot[red, mark=ball] coordinates {({pi/4}, {ln(2)/2})} node[above left] {$\theta=\pi/2$};
\addplot[red, mark=ball] coordinates {(ln(2), 0)} node[above left] {$\theta=\pi$};
\end{axis}
\end{tikzpicture}

In particular we can see that Leibniz series is also in there for $\theta=\frac\pi 2$ with $x=1-\frac 13 + \frac 15 - ... =\frac \pi 4$.
That limit point has $y=\frac 12 - \frac 14 + \frac 16 - ... = \frac 12(1-\frac 12 +\frac 13 - ...)= \frac 12 \ln 2$, which is half of the Alternating harmonic series.