- #1
Determinant of vector of AXB for 3-D
- Thread starter dpa
- Start date
-
- Tags
- Determinant Vector
In summary, the conversation discusses proving the equation aXb=|a||b|sin(theta) and its relation to the determinant and norm of a vector in R^n. It is mentioned that this proof does not directly prove what AXB is, but rather proves that it is equal to nhat*length, where length is |AXB|.
- #2
DonAntonio
- 606
- 2
dpa said:Hi all,
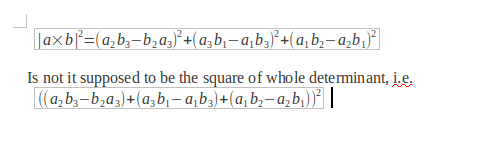
This is a beginning step in proving aXb=|a||b|sin(theta)
thank you
Assuming that expression with a's is the determinant, then yes: it must be the whole thing squared.
DonAntonio
- #3
- #4
chiro
Science Advisor
- 4,817
- 134
Hey dpa.
These brackets refer to the norm and the norm of a vector in R^n is simply is the sum of the components squared. [This norm is simply the ||x-0|| for some vector x]
Also you can't use this to prove what AXB is, but you can prove that for some directional normal vector n^ then you can prove that AXB = nhat*length where length is |AXB|.
These brackets refer to the norm and the norm of a vector in R^n is simply is the sum of the components squared. [This norm is simply the ||x-0|| for some vector x]
Also you can't use this to prove what AXB is, but you can prove that for some directional normal vector n^ then you can prove that AXB = nhat*length where length is |AXB|.
- #5
dpa
- 147
- 0
Thank You.
FAQ: Determinant of vector of AXB for 3-D
1. What is the determinant of a vector of AXB for 3-D?
The determinant of a vector of AXB for 3-D is a mathematical operation that calculates the signed volume of a parallelepiped formed by three vectors - A, B, and the cross product of A and B (AXB). It is also known as the scalar triple product.
2. How is the determinant of a vector of AXB for 3-D calculated?
The determinant of a vector of AXB for 3-D can be calculated using the formula: det(AXB) = (A x B) · C, where C is the third vector perpendicular to both A and B. Another method is to use the components of the three vectors and apply the determinant formula for a 3x3 matrix.
3. What is the significance of the determinant of a vector of AXB for 3-D?
The determinant of a vector of AXB for 3-D has various applications in mathematics and physics. It is used to calculate the volume of a parallelepiped, determine whether three vectors are linearly independent, and find the area of a triangle in 3-D space. It is also used in the study of cross products and their properties.
4. How does the determinant of a vector of AXB for 3-D relate to the orientation of vectors?
The determinant of a vector of AXB for 3-D is related to the orientation of vectors in the sense that it determines whether the vectors are pointing in the same direction (positive determinant), opposite direction (negative determinant), or are coplanar (zero determinant). It also indicates the direction of the cross product vector (right-hand rule).
5. Can the determinant of a vector of AXB for 3-D be negative?
Yes, the determinant of a vector of AXB for 3-D can be negative. This occurs when the three vectors are arranged in a counterclockwise orientation. In this case, the volume of the parallelepiped formed is considered to be negative. However, the absolute value of the determinant remains the same regardless of the orientation of the vectors.