borobeauty66
- 26
- 0
problem solved, thanks
Last edited:
I'm not understanding the problem. You have the equation you need, just change r to x. What would k be?borobeauty66 said:...4Gπρ
F =−_______ mrrˆ (this second r^, being a unit vector)
...3
Fx = -kx
Doc Al said:What would k be?
Sure, so in your equation what would it be?borobeauty66 said:k is the force constant.
Doc Al said:Sure, so in your equation what would it be?
That's the solution for the usual simple harmonic motion equation. Since your equation (for gravity) has the same form, it will have the same solution. Compare the two equations you wrote before: What will take the place of 'k' in your equation?borobeauty66 said:k = mω^2
Right.We haven't been given the values for anything, we're supposed to find the expression in a format of algerbra only.
Do you mean F = -kxDoc Al said:That's the solution for the usual simple harmonic motion equation. Since your equation (for gravity) has the same form, it will have the same solution. Compare the two equations you wrote before: What will take the place of 'k' in your equation?
Right.
I mean to take that equation and compare it to the one you wrote for your gravity problem. What would be the equivalent to k?borobeauty66 said:Do you mean F = -kx
Doc Al said:I mean to take that equation and compare it to the one you wrote for your gravity problem. What would be the equivalent to k?
You shouldn't have to rearrange anything, just read it off.borobeauty66 said:OK give me a few minutes. I'm not very quite when it comes to rearranging and combing equations.
Doc Al said:You shouldn't have to rearrange anything, just read it off.
Your equation has the form: Force = (some constant) x, what's that constant? (It's much easier than you think!)
I'd say so. You know the solution for the standard SHM problem of a mass on a spring. So you want to compare the equations, since the same equations have the same solutions.borobeauty66 said:I'm over-complcating things then?
Almost! (You left out the mass.) But that's exactly the right idea.borobeauty66 said:Not sure if my thinking is correct.
k = 4Gπρ/3
Doc Al said:Almost! (You left out the mass.) But that's exactly the right idea.
Well, what's the period for the standard SHM equation? (In terms of k.)borobeauty66 said:Oh yes, mass sorry, so,
k = 4Gπρm/3
Ok, I'm with you up to hear, just unsure how this applies to period of motion, which is what the question asks for.
Doc Al said:Well, what's the period for the standard SHM equation? (In terms of k.)
Well, you want the period. But you can express the period in terms of the frequency.borobeauty66 said:You mean the frequency? ω?
Doc Al said:Well, you want the period. But you can express the period in terms of the frequency.
Good.borobeauty66 said:Oh I see, the period, t.
So, since ω = 2π/t
t =2π/ω (is this correct? as i say, I'm terrible as rearranging equations)
Now use the expression for ω.Not sure where to go from here.
You forgot the square.borobeauty66 said:Hmmm, If I were to make F = -k x
into F= - mw^2 x
and then
F = -m (2π/t) x
Lets keep it real simple. Forget your gravity problem for the moment. You have the SHM relationship F = -kx. Tell me the period in terms of k and m.and then rearrange to make t the subject, wouldn't this give me the period?
Doc Al said:You forgot the square.
Lets keep it real simple. Forget your gravity problem for the moment. You have the SHM relationship F = -kx. Tell me the period in terms of k and m.
Yes. You already have the solution. From post #5, solve for ω in terms of m and k. And then use what you told me in post #19 to get period in terms of ω and then m and k. When all is said and done, I want to see an expression for period in terms of m and k only.borobeauty66 said:So, F = -k x
-k = F/x
That makes
-mw^2 = f/x
-w = square root of f/x +m
Am i going in the wrong direction?
Doc Al said:Good. Now simplify that as much as you can.
Doc Al said:Almost! (You left out the mass.) But that's exactly the right idea.
Not quite sure what you mean. In any case, when you simplify your expression in post #25, the mass cancels out.borobeauty66 said:Just realized that mass isn't part of the 4Gpi p/3 equation, it comes later.
Doc Al said:Not quite sure what you mean. In any case, when you simplify your expression in post #25, the mass cancels out.
They both have the same form: Force = -(some constant)x, where x is the displacement from some equilibrium point. That's all that matters.borobeauty66 said: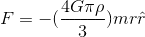
This is the original equation.
I'm now wondering if
F = -k x is infact equal to the above?
Those expressions are identical! (Except for the unneeded unit vector.) For the same reason that (a/b)x is the same as (ax/b).borobeauty66 said:What I meant by saying the equation was wrong was in your #3 post you put the equation wrong. In actual fact the mass should come after the division. Thus
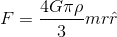
and not
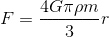
Doc Al said:Those expressions are identical! (Except for the unneeded unit vector.) For the same reason that (a/b)x is the same as (ax/b).