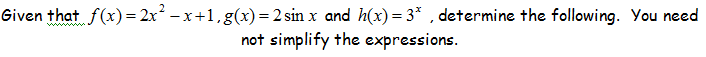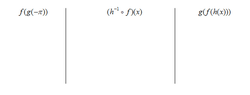Alaba27
- 18
- 0
This question is killing me. I'm finding it difficult to do and it's a problem with my homework.
Given that $$f(x)=2x^2-x+1,\,g(x)=2\sin(x)\text{ and }h(x)=3^x$$, determine the following. You need not simplify the expressions.
$$f(g(-\pi))=?$$
$$\left(h^{-1}\circ f \right)(x)=?$$
$$g(f(h(x)))=?$$
View attachment 846
View attachment 847
I am so lost right now. Please help!
Given that $$f(x)=2x^2-x+1,\,g(x)=2\sin(x)\text{ and }h(x)=3^x$$, determine the following. You need not simplify the expressions.
$$f(g(-\pi))=?$$
$$\left(h^{-1}\circ f \right)(x)=?$$
$$g(f(h(x)))=?$$
View attachment 846
View attachment 847
I am so lost right now. Please help!
Attachments
Last edited by a moderator: