vcsharp2003
- 913
- 179
- Homework Statement
- What will be the equivalent Young's Modulus of the system shown in diagram below.
- Relevant Equations
- Y= stress/strain
We need to find a single wire supporting the load. But, when I think about it there can so many different types of materials we could use for the single wire and each of these single wires would have a different Young's Modulus. So, I don't get what equivalent means here?
Anyways, I get the following equations assuming each wire will extend by a different amount and also tensions in each wire are taken as different. I am not sure if this approach is correct i.e. whether wires would have different tensions and extend by different amounts.
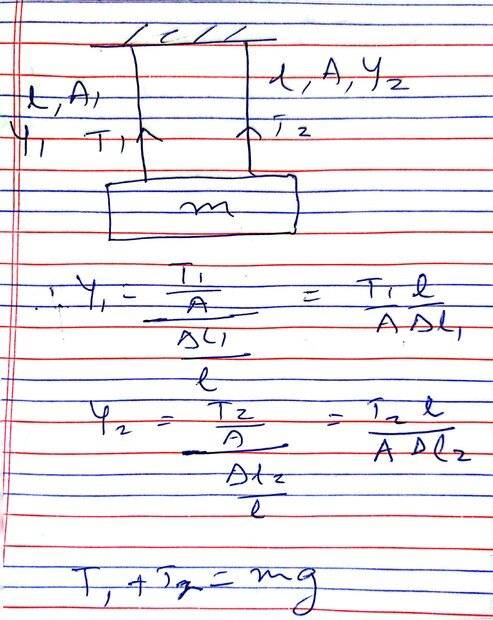

Anyways, I get the following equations assuming each wire will extend by a different amount and also tensions in each wire are taken as different. I am not sure if this approach is correct i.e. whether wires would have different tensions and extend by different amounts.