Determine exact solutions to trig equation with graphing calculator

Click For Summary

Discussion Overview

The discussion revolves around determining the exact solutions to a trigonometric equation using a graphing calculator, specifically focusing on solutions within the interval [0, 360) degrees. Participants explore how to interpret the graph to identify the number of solutions.

Discussion Character

  • Exploratory, Technical explanation, Homework-related

Main Points Raised

  • One participant describes their approach to inputting the function into a TI-83+ calculator and expresses interest in determining the exact solutions.
  • Another participant suggests counting the roots visible on the graph to find the solutions.
  • A participant questions whether the graph is plotted in radians, noting that it appears to show 7 roots.
  • There is clarification that the graph was plotted in radians without converting to degrees, which affects the counting of roots.
  • One participant acknowledges seeing 7 points where y=0, but later corrects themselves to state they see 6 points after considering the domain restriction.
  • Participants discuss the importance of not counting the root at x=2π, as it is excluded from the specified domain.

Areas of Agreement / Disagreement

Participants do not reach a consensus on the exact number of solutions initially, as there is a discrepancy between counting 6 and 7 roots. However, there is agreement on the importance of the domain in determining which roots to count.

Contextual Notes

The discussion includes assumptions about the graphing method and the interpretation of roots, which depend on the choice of radians versus degrees. The exclusion of x=2π from the domain is also a critical factor in the counting of solutions.

Who May Find This Useful

Students or individuals learning about trigonometric equations and their graphical representations, particularly those using graphing calculators for homework or study purposes.

estex198
Messages
14
Reaction score
0
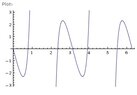
Im trying to determine the exact solutions (in degrees) to the trig equation shown below. I'm only interested in solutions over the interval [0, 360) . In my ti-83+, I input the function as y= 6(1/cos(X))^2*tan(X)-12tan(X). If I already know the number of solutions is 6, how can I tell this from the graph??
 

Attachments

  • Screenshot from 2014-02-05 04:03:01.jpg
    Screenshot from 2014-02-05 04:03:01.jpg
    25.1 KB · Views: 107
Mathematics news on Phys.org
estex198 said:
If I already know the number of solutions is 6, how can I tell this from the graph??

Count them?
 

Attachments

  • estex198.jpg
    estex198.jpg
    6.7 KB · Views: 134
Is that graph plotted using radians? Still it looks like 7.
 
estex198 said:
Is that graph plotted using radians? Still it looks like 7.

Yes, I did not convert to degrees, I just let the domain be $$0\le x<2\pi$$ which means you do not count the root at $x=2\pi$.
 
Ok great! So now I see y=0 (or roots as you refer to them) at 7 points. Thanks for the help!
 
estex198 said:
Ok great! So now I see y=0 (or roots as you refer to them) at 7 points. Thanks for the help!

You don't want to count the root at $x=2\pi$ because this is excluded from the domain.
 
MarkFL said:
You don't want to count the root at $x=2\pi$ because this is excluded from the domain.

Forgive me, I meant to say I see y=0 at 6 points. Thanks for reminding me of the domain.
 

Similar threads

Undergrad Finding the explicit solution of a trig equation
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Equation to graph a sine wave that acts like a point on a unit circle
  • · Replies 8 ·
Replies
8
Views
2K
MHB How can I determine the biggest trig value without a calculator?
  • · Replies 4 ·
Replies
4
Views
2K
MHB More than one equation for a given Trig Graph?
  • · Replies 5 ·
Replies
5
Views
3K
MHB Approximating Trig Values using the Unit Circle
  • · Replies 11 ·
Replies
11
Views
3K
MHB Finding equation from logarithmic graph
  • · Replies 6 ·
Replies
6
Views
3K
MHB Helping my daughter study for a Trig test....
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Fun with graphs and calculators
  • · Replies 1 ·
Replies
1
Views
2K
MHB Solve Trig Equation Graphically & Algebraically: Why Different Answers?
  • · Replies 11 ·
Replies
11
Views
6K
MHB Emma's question at Yahoo Answers regarding solving a trigonometric equation
  • · Replies 2 ·
Replies
2
Views
2K