- #1
mhrob24
- 53
- 9
I work in injection molding and I am looking to make some sort of standard for how many bolts are needed to secure what we call a "manifold spacer block". We are constantly battling each other about blocks being under or over secured, and as a manufacturing engineer, I am interested in knowing how much weight a single 3/4-10 UNC bolt can hold before it snaps in half. Below are some images that will hopefully help whoever is reading this understand the system at hand in this problem:
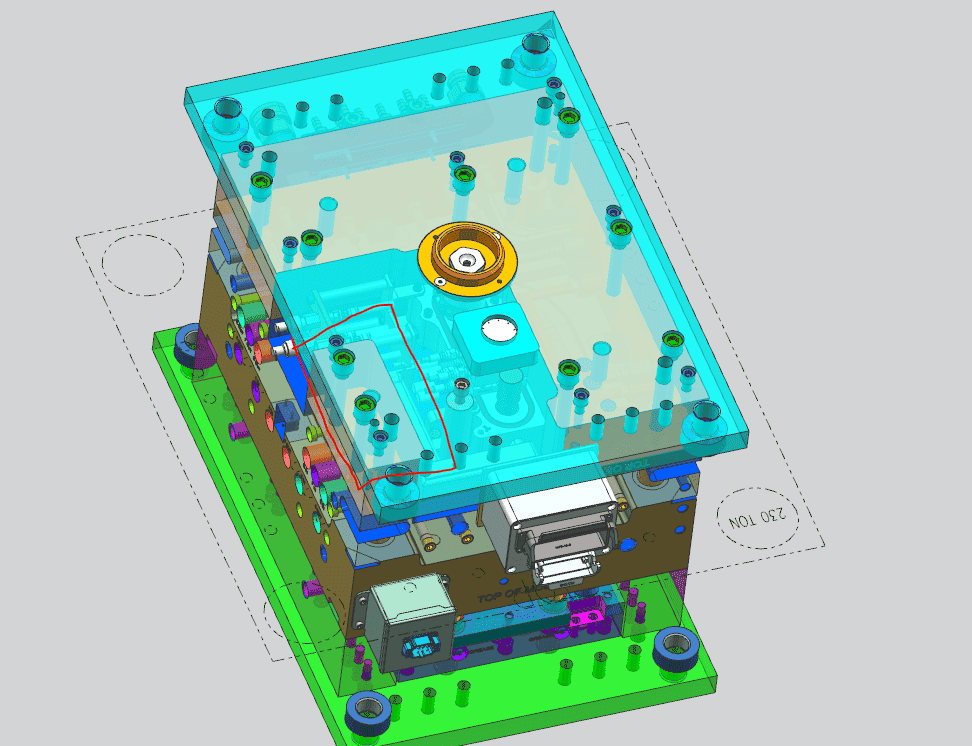
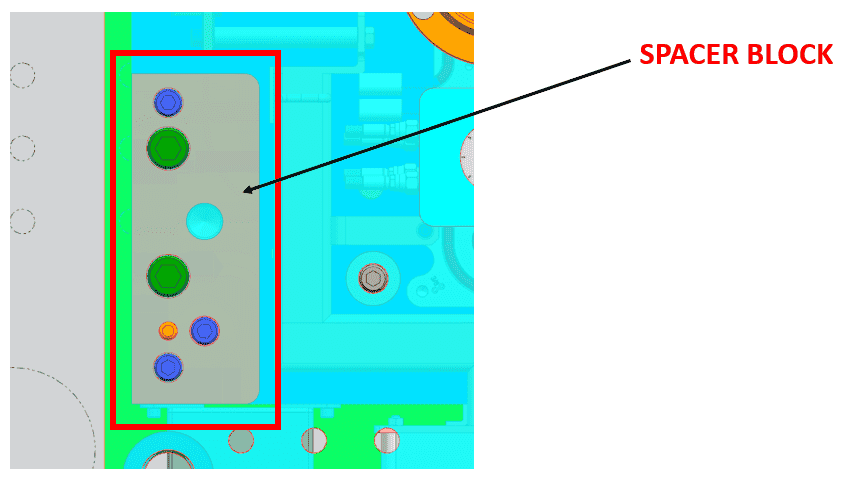
Side view of the system (this is how the tool is ran in the injection mold press when processing parts. The clamp plates are bolted onto the press platen so the tool hangs sideways as shown):
If I can figure this out, knowing how much weight a single bolt can hold, I can create a chart with a range of weights and the minimum number of bolts needed to secure that block (ex: spacer blocks weighing between 250 - 750lbs = two 3/4 - 10 UNC bolts).
I'm pretty sure the first step would be to calculate the shear stress (double shear in this case?) acting on the bolt using a free body diagram — which after some google searching, seems fairly straight forward.
However, what do I do with that value after obtaining it? The charts that I found for socket head cap screws list the "shear STRENGTH" for a single 3/4 - 10 UNC bolt aa 45,000lbs...I know I'm not thinking about this correctly, but when I read that, I am thinking that the chart is telling me that a single 3/4 - 10 UNC bolt can withstand 45,000lbs of shear load before snapping in half...which can't be possible.
Also, how does the location of the bolt on the block come into play in this equation? I'd assume that if you have a bolt directly in the center of a block, its going to be able to withstand a greater shear load versus if it was all the way at the end of the block...right?
What am I not understanding? I am going in the right direction? After calculating the shear stress on the bolt, how do I find out if this shear stress is tolerable for the bolt or if this is too much and it will cause the bolt to snap?
Not looking for any provided answers, just some guidance / direction in terms of how I should go about achieving my goal.
PS: I'm assuming the force of the clamp plate acting on the spacer block would be negligible in this case because the clamp plate is bolted onto multiple spacer blocks, so the force on a single spacer block would more than likely not impact the equation, especially if a safety factor is included in the shear load equation.
Side view of the system (this is how the tool is ran in the injection mold press when processing parts. The clamp plates are bolted onto the press platen so the tool hangs sideways as shown):
I'm pretty sure the first step would be to calculate the shear stress (double shear in this case?) acting on the bolt using a free body diagram — which after some google searching, seems fairly straight forward.
However, what do I do with that value after obtaining it? The charts that I found for socket head cap screws list the "shear STRENGTH" for a single 3/4 - 10 UNC bolt aa 45,000lbs...I know I'm not thinking about this correctly, but when I read that, I am thinking that the chart is telling me that a single 3/4 - 10 UNC bolt can withstand 45,000lbs of shear load before snapping in half...which can't be possible.
Also, how does the location of the bolt on the block come into play in this equation? I'd assume that if you have a bolt directly in the center of a block, its going to be able to withstand a greater shear load versus if it was all the way at the end of the block...right?
What am I not understanding? I am going in the right direction? After calculating the shear stress on the bolt, how do I find out if this shear stress is tolerable for the bolt or if this is too much and it will cause the bolt to snap?
Not looking for any provided answers, just some guidance / direction in terms of how I should go about achieving my goal.
PS: I'm assuming the force of the clamp plate acting on the spacer block would be negligible in this case because the clamp plate is bolted onto multiple spacer blocks, so the force on a single spacer block would more than likely not impact the equation, especially if a safety factor is included in the shear load equation.
