Determine the Average Rate of Change

[eleventhxhour]

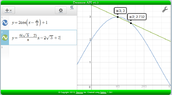
Determine the average rate if change of the function y = 2cos(x - $\pi$/3) + 1 for the interval $\pi$/3 $\le$ x $\le$ $\pi$/2

I tried finding the exact values of the two (0 and 0.5) and subbing them into the AROC equation but I keep getting the wrong answer (1.4)

 

[MarkFL]

We find:

\(\displaystyle \frac{\Delta y}{\Delta x}=\frac{y\left(\dfrac{\pi}{2}\right)-y\left(\dfrac{\pi}{3}\right)}{\dfrac{\pi}{2}-\dfrac{\pi}{3}}=\frac{\left(2\cos\left(\dfrac{\pi}{6}\right)+1\right)-\left(2\cos\left(0\right)+1\right)}{\dfrac{\pi}{6}}=\frac{6\left(\sqrt{3}-1\right)}{\pi}\approx1.39811405542801\)

 

[eleventhxhour]

We find:

\(\displaystyle \frac{\Delta y}{\Delta x}=\frac{y\left(\dfrac{\pi}{2}\right)-y\left(\dfrac{\pi}{3}\right)}{\dfrac{\pi}{2}-\dfrac{\pi}{3}}=\frac{\left(2\cos\left(\dfrac{\pi}{6}\right)+1\right)-\left(2\cos\left(0\right)+1\right)}{\dfrac{\pi}{6}}=\frac{6\left(\sqrt{3}-1\right)}{\pi}\approx1.39811405542801\)

Okay, that's what I got. The textbook has it as -0.5157 so I guess it's just wrong?

 

[MarkFL]

We both made an error...it should be:

\(\displaystyle \frac{\Delta y}{\Delta x}=\frac{6\left(\sqrt{3}-2\right)}{\pi}\approx-0.511745261674736\)

I discovered my error when graphing the function and the resulting secant line:

View attachment 3547

 

[CellCoree]

I would approach this problem by first clarifying the units of measurement for both the function and the interval. In this case, the function y represents a unitless quantity, while the interval x is measured in radians. This is important to note when calculating the average rate of change.

To determine the average rate of change, we can use the formula: AROC = (f(b) - f(a)) / (b - a), where f(b) and f(a) represent the values of the function at the upper and lower bounds of the interval, respectively.

In this case, we have f(b) = 2cos(π/2 - π/3) + 1 = 1 and f(a) = 2cos(π/3 - π/3) + 1 = 2. The upper bound of our interval is π/2 and the lower bound is π/3. Substituting these values into the AROC formula, we get:

AROC = (1 - 2) / (π/2 - π/3) = -1 / π/6 = -6/π

Therefore, the average rate of change for the given function and interval is -6/π units per radian. This means that for every radian increase in the input variable x, the output variable y decreases by an average of 6/π units.

It is important to carefully check the calculations and units to ensure the correct answer is obtained. If you continue to get a different answer, I would recommend double-checking the values used and the order of operations. Alternatively, you could also try using a graphing calculator to plot the function and visually determine the slope of the line between the two points.